《2025年人教金学典同步解析与测评八年级数学上册人教版云南专版》

25. (8 分)如图,在 Rt△ABC 中,∠A = 90°,CD,BE 是角平分线,它们相交于点 F,EG // BC,CG ⊥ EG,垂足为 G.
(1)求∠BFD 的度数.
(2)求证：∠ADC = ∠GCD.

答案：
(1)解:∠BFD=45°.
(2)证明:因为EG//BC,CG⊥EG,所以CG⊥BC,所以∠BCG=90°.因为CD平分∠ACB,所以∠ACD=∠BCD.因为∠ADC+∠ACD=∠GCD+∠BCD=90°,所以∠ADC=∠GCD.

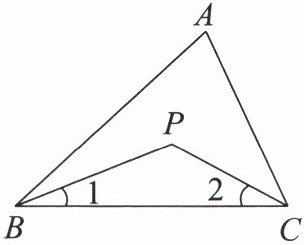
26. (8 分)如图,P 是△ABC 内一点,连接 PB,PC.
(1)当∠1 = $\frac{1}{2}$∠ABC,∠2 = $\frac{1}{2}$∠ACB 时,∠P 与∠A 之间的数量关系是______.
(2)当∠1 = $\frac{1}{3}$∠ABC,∠2 = $\frac{1}{3}$∠ACB 时,∠P 与∠A 的数量关系是什么？请说明理由.
(3)当∠1 = $\frac{1}{n}$∠ABC,∠2 = $\frac{1}{n}$∠ACB 时,请直接写出∠P 与∠A 的数量关系.

答案： 解:
(1)∠1+∠2=$\frac{1}{2}×(180° - ∠A)$=90° - $\frac{1}{2}∠A$,所以∠P=180° - (∠1+∠2)=180° - $(90° - \frac{1}{2}∠A)$=90° + $\frac{1}{2}∠A$.故答案为∠P=90° + $\frac{1}{2}∠A$.
(2)∠P=120° + $\frac{1}{3}∠A$.理由如下:因为∠1=$\frac{1}{3}∠ABC$,∠2=$\frac{1}{3}∠ACB$,所以∠1+∠2=$\frac{1}{3}(180° - ∠A)$=60° - $\frac{1}{3}∠A$,所以∠P=180° - (∠1+∠2)=180° - $(60° - \frac{1}{3}∠A)$=120° + $\frac{1}{3}∠A$.
(3)∠P=180° - $\frac{180°}{n}$ + $\frac{1}{n}∠A$.

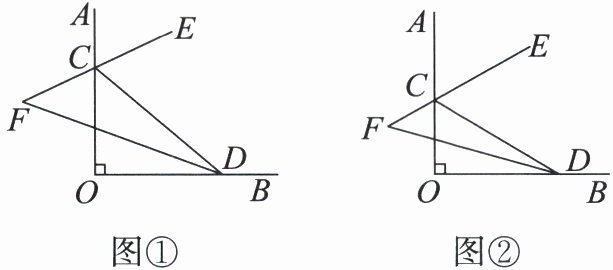
27. (12 分)如图,∠AOB = 90°,点 C,D 分别在射线 OA,OB 上,CE 是∠ACD 的平分线,CE 的反向延长线与∠CDO 的平分线交于点 F.
(1)当∠OCD = 50°(如图①)时,求∠F 的度数.
(2)当 C,D 在射线 OA,OB 上任意移动时(不与点 O 重合)(如图②),∠F 的大小是否变化？请说明理由.

答案： 解:
(1)因为∠AOB=90°,∠OCD=50°,所以∠CDO=40°,∠ACD=130°.因为CE是∠ACD的平分线,DF是∠CDO的平分线,所以∠ECD=65°,∠CDF=20°.因为∠ECD=∠F+∠CDF,所以∠F=45°.
(2)∠F的大小不变.理由如下:因为∠AOB=90°,所以∠CDO=90° - ∠OCD,∠ACD=180° - ∠OCD.因为CE是∠ACD的平分线,DF是∠CDO的平分线,所以∠ECD=90° - $\frac{1}{2}∠OCD$,∠CDF=45° - $\frac{1}{2}∠OCD$.因为∠ECD=∠F+∠CDF,所以∠F=45°.所以∠F的大小不变.