1. 在一个不透明的盒子中装有 $ a $ 个除颜色外完全相同的球,这 $ a $ 个球中只有 2 个红球. 若每次将球充分搅匀后,任意摸出 1 个球记下颜色后再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在 $ 10\% $ 左右,则 $ a $ 的值大约为(
A.10
B.20
C.18
D.25
B
).A.10
B.20
C.18
D.25
答案:
1.B
2. 如图,一只蚂蚁在树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,则它获得食物的概率是(
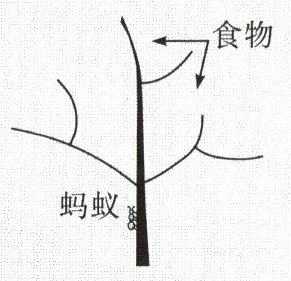
A.$\dfrac{1}{6}$
B.$\dfrac{1}{4}$
C.$\dfrac{1}{3}$
D.$\dfrac{1}{2}$
C
).
A.$\dfrac{1}{6}$
B.$\dfrac{1}{4}$
C.$\dfrac{1}{3}$
D.$\dfrac{1}{2}$
答案:
2.C
3. “二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”,小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小明. 小文将它们背面朝上放在桌面上(邮票背面完全相同),将邮票洗匀后,让小明从中随机抽取两张,则小明抽到的两张邮票恰好是“立夏”和“秋分”的概率是(
A.$\dfrac{1}{2}$
B.$\dfrac{2}{3}$
C.$\dfrac{1}{8}$
D.$\dfrac{1}{6}$
D
).A.$\dfrac{1}{2}$
B.$\dfrac{2}{3}$
C.$\dfrac{1}{8}$
D.$\dfrac{1}{6}$
答案:
3.D
4. 有两把不同的锁和三把钥匙,其中两把钥匙能打开同一把锁,第三把钥匙能打开另一把锁. 任意取出一把钥匙去开任意的一把锁,一次能打开锁的概率是(
A.$\dfrac{1}{2}$
B.$\dfrac{1}{3}$
C.$\dfrac{1}{4}$
D.$\dfrac{2}{3}$
A
).A.$\dfrac{1}{2}$
B.$\dfrac{1}{3}$
C.$\dfrac{1}{4}$
D.$\dfrac{2}{3}$
答案:
4.A
5. 三名初三学生坐在仅有的三个座位上,起身后重新就座,恰好有两名同学没有坐回原座位的概率是(
A.$\dfrac{1}{9}$
B.$\dfrac{1}{6}$
C.$\dfrac{1}{4}$
D.$\dfrac{1}{2}$
D
).A.$\dfrac{1}{9}$
B.$\dfrac{1}{6}$
C.$\dfrac{1}{4}$
D.$\dfrac{1}{2}$
答案:
5.D
6. 投掷一枚质地均匀的骰子两次,向上一面的点数依次记为 $ a,b $,则关于 $ x $ 的方程 $ x^{2}+ax + b = 0 $ 有解的概率是(
A.$\dfrac{1}{2}$
B.$\dfrac{1}{3}$
C.$\dfrac{8}{15}$
D.$\dfrac{19}{36}$
D
).A.$\dfrac{1}{2}$
B.$\dfrac{1}{3}$
C.$\dfrac{8}{15}$
D.$\dfrac{19}{36}$
答案:
6.D
7. 学生甲与学生乙玩一种转盘游戏. 两个完全相同的转盘如图所示,每个转盘被分成面积相等的四个区域,分别用数字“1”“2”“3”“4”表示. 固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若指针指向扇形的分界线,则都重转一次. 在该游戏中乙获胜的概率是(
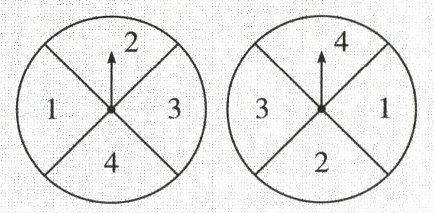
A.$\dfrac{1}{4}$
B.$\dfrac{1}{2}$
C.$\dfrac{3}{4}$
D.$\dfrac{5}{6}$
C
).
A.$\dfrac{1}{4}$
B.$\dfrac{1}{2}$
C.$\dfrac{3}{4}$
D.$\dfrac{5}{6}$
答案:
7.C
查看更多完整答案,请扫码查看


