《2025年家庭作业九年级数学上册北师大版》

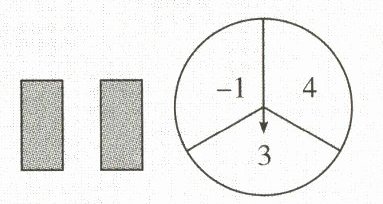
20. （10 分）小云玩抽卡片和转转盘游戏. 有两张正面分别标有数字 $1$，$2$ 的不透明卡片，背面完全相同；转盘被平均分成 $3$ 个相同的扇形，并分别标有数字 $-1$，$3$，$4$（如图所示）. 小云把卡片背面朝上洗匀后从中随机抽出一张，记下卡片上的数字；然后转动转盘，转盘停止后，记下指针所在区域的数字（若指针指向分界线，则重转一次，直到指针指向某一区域为止）.
（1）请用列表或树状图的方法（只选其中一种）表示出两次所得数字可能出现的所有结果；
（2）求出两个数字之积为负数的概率.

答案：
20.解：
(1)列表如下：
或画树状图如下：

可能出现的结果共6种，它们出现的可能性相同。
(2)两数之积为负数的情况共有2种可能，所以两数之积为负数的概率为$\frac{2}{6}$ = $\frac{1}{3}$。

21. （10 分）一学校为了绿化校园环境，从某园林公司购买了一批树苗. 园林公司规定：如果购买树苗不超过 $60$ 棵，每棵售价为 $120$ 元；如果购买树苗超过 $60$ 棵，每增加 $1$ 棵，所出售的这批树苗每棵售价均降低 $0.5$ 元，但每棵树苗最低售价不得少于 $100$ 元. 该校最终向园林公司支付树苗款 $8800$ 元. 请问该校一共购买了多少棵树苗？

答案： 21.解：因为60棵树苗售价为120×60 = 7200(元) ＜ 8800元，所以该校购买树苗超过60棵。
设该校共购买了x棵树苗，由题意得x[120 - 0.5(x - 60)] = 8800。解得x₁ = 220，x₂ = 80。
当x₁ = 220时，120 - 0.5×(220 - 60) = 40 ＜ 100，所以x₁ = 220不合题意，舍去；
当x₂ = 80时，120 - 0.5×(80 - 60) = 110 ＞ 100，符合题意。
所以x = 80。故该校共购买了80棵树苗。

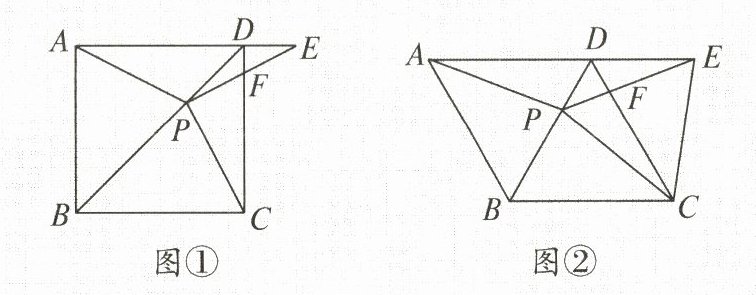
22. （10 分）如图①，在正方形 $ABCD$ 中，$P$ 是 $BD$ 上的一点，点 $E$ 在 $AD$ 的延长线上，且 $PA = PE$，$PE$ 交 $CD$ 于点 $F$.
（1）证明：$PC = PE$；
（2）求 $\angle CPE$ 的度数；
（3）如图②，把正方形 $ABCD$ 改为菱形 $ABCD$，其他条件不变，当 $\angle ABC = 120^{\circ}$ 时，连接 $CE$，试探究线段 $AP$ 与线段 $CE$ 的数量关系，并说明理由.

答案： 22.
(1)证明：
∵四边形ABCD是正方形，
∴AD = CD，∠ADP = ∠CDP。
∵DP = DP，
∴△ADP≌△CDP，
∴PA = PC。
∵PA = PE，
∴PC = PE。
(2)解：
∵△ADP≌△CDP，
∴∠DAP = ∠DCP。
∵PA = PE，
∴∠DAP = ∠E，
∴∠DCP = ∠E。
∵∠PFC = ∠DFE，∠EDF = 90°，
∴∠CPE = ∠EDF = 90°。
(3)解：AP = CE。理由如下：
∵四边形ABCD是菱形，∠ABC = 120°，
∴∠ADC = 120°，
∴∠EDC = 60°。
同理可得∠CPE = ∠EDF = 60°。
易知PC = PE，
∴△PCE是等边三角形。
∵PA = PE，
∴AP = CE。