7. 如图,某小区计划在一块长为 $32\mathrm{m}$、宽为 $20\mathrm{m}$ 的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为 $570\mathrm{m}^{2}$,若设道路的宽为 $x\mathrm{m}$,则下面所列方程正确的是(
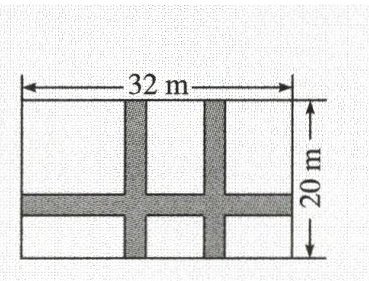
A.$(32 - 2x)(20 - x)=570$
B.$32x + 2×20x = 32×20 - 570$
C.$(32 - 2x)(20 - x)=32×20 - 570$
D.$32x + 2×20x - 2x^{2}=570$
A
).
A.$(32 - 2x)(20 - x)=570$
B.$32x + 2×20x = 32×20 - 570$
C.$(32 - 2x)(20 - x)=32×20 - 570$
D.$32x + 2×20x - 2x^{2}=570$
答案:
7.A
8. 若菱形的周长为 $4\sqrt{2}$,面积为 $\sqrt{2}$,则菱形的高为(
A.$\sqrt{2}$
B.$1$
C.$\sqrt{3}$
D.$2$
B
).A.$\sqrt{2}$
B.$1$
C.$\sqrt{3}$
D.$2$
答案:
8.B
9. 小亮与小齐学习概率初步知识后设计如下游戏:小亮手中有方块 $10$,$8$,$6$ 三张扑克牌,小齐手中有方块 $9$,$7$,$5$ 三张扑克牌. 每人从各自手中取一张牌进行比较,数字大的本局获胜,每次取的牌不能放回. 若本次游戏采用三局两胜制,即胜 $2$ 局或 $3$ 局者为本次游戏获胜者. 当小亮的三张牌出牌顺序为先出 $6$,再出 $8$,最后出 $10$ 时,小齐随机出牌应对,则小齐本次游戏获胜的概率是(
A.$\frac{1}{6}$
B.$\frac{1}{2}$
C.$\frac{1}{9}$
D.$\frac{1}{3}$
A
).A.$\frac{1}{6}$
B.$\frac{1}{2}$
C.$\frac{1}{9}$
D.$\frac{1}{3}$
答案:
9.A
10. 我们都知道,四边形具有不稳定性,老师制作了一个正方形教具用于课堂教学,数学课代表小亮在取道具时不小心使教具发生了形变(如图),若正方形道具边长为 $10\mathrm{cm}$,$\angle D' = 30^{\circ}$,则四边形的面积减少了(
A.$50\mathrm{cm}^{2}$
B.$50\sqrt{2}\mathrm{cm}^{2}$
C.$100\mathrm{cm}^{2}$
D.$100\sqrt{2}\mathrm{cm}^{2}$
A
).A.$50\mathrm{cm}^{2}$
B.$50\sqrt{2}\mathrm{cm}^{2}$
C.$100\mathrm{cm}^{2}$
D.$100\sqrt{2}\mathrm{cm}^{2}$
答案:
10.A
11. 某企业五月份的利润是 $25$ 万元,预计七月份的利润将达到 $36$ 万元. 设平均月增长率为 $x$,根据题意所列方程是
25(1+x)²=36
.
答案:
11.25(1+x)²=36
12. 如图,在菱形 $ABCD$ 中,$AC$ 交 $BD$ 于点 $O$,$DE\perp BC$ 于 $E$,连接 $OE$,若 $\angle ABC = 140^{\circ}$,则 $\angle OED =$

20°
.
答案:
12.20°
13. 甲、乙、丙三名同学打乒乓球,想通过“手心手背”游戏来决定其中哪两人先打. 规则如下:三人同时各用一只手随机出示手心或手背,若只有两人手势相同(都是手心或都是手背),则这两人先打;若三人手势相同,则重新决定. 通过一次“手心手背”游戏能决定甲打乒乓球的概率是
$\frac{1}{2}$
.
答案:
13.$\frac{1}{2}$
14. 如果任意选择一对有序整数 $(m,n)$,其中 $|m|\leq1$,$|n|\leq3$,每一对这样的有序整数对被选择的可能性是相等的,那么关于 $x$ 的方程 $x^{2}+nx + m = 0$ 有两个相等的实数根的概率是
$\frac{1}{7}$
.
答案:
14.$\frac{1}{7}$
15. 设 $\alpha$,$\beta$ 是一元二次方程 $x^{2}+3x - 7 = 0$ 的两个根,则 $\alpha^{2}+4\alpha+\beta=$
4
.
答案:
15.4
查看更多完整答案,请扫码查看


