《2025年新课标学习方法指导丛书九年级数学上册浙教版》

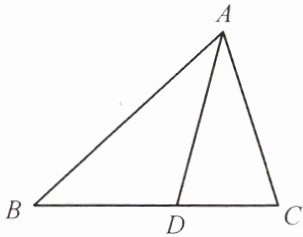
13. 如图,AD 是$\triangle ABC$的角平分线,则$AB:AC$等于(A)

A.$BD:CD$
B.$AD:CD$
C.$BC:AD$
D.$BC:AC$

答案： A

14. 如图,线段AB 上存在一点 C,满足$AC:CB= CB:AB= k$.
(1)求k的值.
(2)如果三条线段a,b,c满足$a:b= b:c= k$,这三条线段能否构成三角形？如果能,请指出三角形的形状；如果不能,请说明理由.

答案：
(1)设$AB=1$，由$CB:AB=k$得$CB=k$。
由$AC:CB=k$得$AC=k\cdot CB=k^2$。
因为$AC+CB=AB$，所以$k^2 + k = 1$，即$k^2 + k - 1 = 0$。
解得$k=\frac{-1\pm\sqrt{5}}{2}$，因$k＞0$，故$k=\frac{\sqrt{5}-1}{2}$。
(2)由$a:b=b:c=k$，得$a=kb$，$c=\frac{b}{k}$。
则$a + b=kb + b=b(k + 1)$，又由
(1)知$k + 1=\frac{1}{k}$，故$a + b=\frac{b}{k}=c$。
因三角形两边之和需大于第三边，而$a + b=c$，故不能构成三角形。
(1)$k=\frac{\sqrt{5}-1}{2}$；
(2)不能构成三角形。

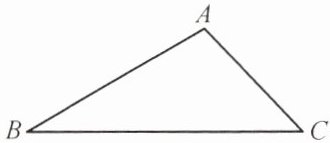
15. 如图,在$\triangle ABC$中,已知$\angle B= 30^{\circ},\angle C= 45^{\circ}.$
(1)求$\frac{AB}{AC}$.
(2)求$AB:AC:BC$.

答案：
(1)过点A作AD⊥BC于点D，设AD=h。
在Rt△ABD中，∠B=30°，则AB=AD/sin30°=h/(1/2)=2h。
在Rt△ACD中，∠C=45°，则AC=AD/sin45°=h/(√2/2)=√2 h。
∴AB/AC=2h/(√2 h)=√2。
(2)由
(1)得AB=2h，AC=√2 h。
在Rt△ABD中，BD=AB·cos30°=2h·(√3/2)=√3 h。
在Rt△ACD中，CD=AD=h，
∴BC=BD+CD=√3 h + h=h(√3 +1)。
∴AB:AC:BC=2h : √2 h : h(√3 +1)=2 : √2 : (√3 +1)。
(1)√2
(2)2 : √2 : (√3 +1)