13. 如图,若干全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环还需
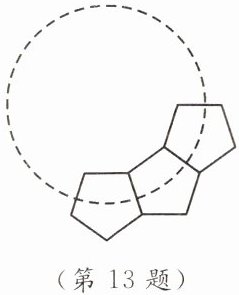
2
个五边形.
答案:
2
14. 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,$\triangle ABC$的顶点都在格点上.设定$AB$边如图所示,则$\triangle ABC$是直角三角形的个数为

6
.
答案:
6
15. 如图,图1,图2,图3,…,图$n$分别是$\odot O$的内接正三角形$ABC$,正四边形$ABCD$,正五边形$ABCDE$,…,正$n$边形$ABCD$,…,点$M$,$N$分别从点$B$,$C$开始以相同的速度在$\odot O$上逆时针运动.
(1)图1中$\angle APN$的度数是
(2)试探索$\angle APN$的度数与正多边形边数$n$的关系:
(1)图1中$\angle APN$的度数是
$60^{\circ}$
,图2中$\angle APN$的度数是$90^{\circ}$
,图3中$\angle APN$的度数是$108^{\circ}$
.(2)试探索$\angle APN$的度数与正多边形边数$n$的关系:
$\angle APN=\frac{(n-2)× 180^{\circ}}{n}$
.(直接写出答案)
答案:
(1)
图1:
$\because \odot O$是正三角形$ABC$的外接圆,点$M$,$N$分别从点$B$,$C$开始以相同的速度在$\odot O$上逆时针运动,
$\therefore \stackrel\frown{BM}=\stackrel\frown{CN}$,
$\therefore \stackrel\frown{CM}=\stackrel\frown{BN}$,
$\therefore CM=BN$,
又$\because AB=AC$,$\angle BAC=\angle ABN=\angle ACM=60^{\circ}$,
$\therefore \triangle ACM\cong\triangle ABN(SAS)$,
$\therefore \angle CAM=\angle ABN$,
$\therefore \angle APN=\angle ABN+\angle BAP=\angle CAM+\angle BAP=\angle BAC=60^{\circ}$。
图2:
$\because \odot O$是正四边形$ABCD$的外接圆,点$M$,$N$分别从点$B$,$C$开始以相同的速度在$\odot O$上逆时针运动,
$\therefore \stackrel\frown{BM}=\stackrel\frown{CN}$,
$\therefore \stackrel\frown{CM}=\stackrel\frown{BN}$,
$\therefore CM=BN$,
又$\because AB=CD$,$\angle ABC=\angle DCM=90^{\circ}$,
$\therefore \triangle ABN\cong\triangle DCM(SAS)$,
$\therefore \angle BAN=\angle CDM$,
$\because \angle CDM+\angle DCM=90^{\circ}$,
$\therefore \angle BAN+\angle DCM=90^{\circ}$,
$\therefore \angle APN=\angle BAN+\angle BAM=\angle BAN+\angle DCM=90^{\circ}$。
图3:
$\because \odot O$是正五边形$ABCDE$的外接圆,点$M$,$N$分别从点$B$,$C$开始以相同的速度在$\odot O$上逆时针运动,
$\therefore \stackrel\frown{BM}=\stackrel\frown{CN}$,
$\therefore \stackrel\frown{CM}=\stackrel\frown{BN}$,
$\therefore CM=BN$,
又$\because AB=AE$,$\angle ABC=\angle E=108^{\circ}$,$\angle ACM=\angle ABN$,
$\therefore \triangle ACM\cong\triangle ABN(SAS)$,
$\therefore \angle CAM=\angle ABN$,
$\therefore \angle APN=\angle ABN+\angle BAP=\angle CAM+\angle BAP=\angle BAE=108^{\circ}$。
故答案为$60^{\circ}$;$90^{\circ}$;$108^{\circ}$。
(2)$\angle APN$的度数与正多边形边数$n$的关系是$\angle APN=\frac{(n-2)× 180^{\circ}}{n}$。
图1:
$\because \odot O$是正三角形$ABC$的外接圆,点$M$,$N$分别从点$B$,$C$开始以相同的速度在$\odot O$上逆时针运动,
$\therefore \stackrel\frown{BM}=\stackrel\frown{CN}$,
$\therefore \stackrel\frown{CM}=\stackrel\frown{BN}$,
$\therefore CM=BN$,
又$\because AB=AC$,$\angle BAC=\angle ABN=\angle ACM=60^{\circ}$,
$\therefore \triangle ACM\cong\triangle ABN(SAS)$,
$\therefore \angle CAM=\angle ABN$,
$\therefore \angle APN=\angle ABN+\angle BAP=\angle CAM+\angle BAP=\angle BAC=60^{\circ}$。
图2:
$\because \odot O$是正四边形$ABCD$的外接圆,点$M$,$N$分别从点$B$,$C$开始以相同的速度在$\odot O$上逆时针运动,
$\therefore \stackrel\frown{BM}=\stackrel\frown{CN}$,
$\therefore \stackrel\frown{CM}=\stackrel\frown{BN}$,
$\therefore CM=BN$,
又$\because AB=CD$,$\angle ABC=\angle DCM=90^{\circ}$,
$\therefore \triangle ABN\cong\triangle DCM(SAS)$,
$\therefore \angle BAN=\angle CDM$,
$\because \angle CDM+\angle DCM=90^{\circ}$,
$\therefore \angle BAN+\angle DCM=90^{\circ}$,
$\therefore \angle APN=\angle BAN+\angle BAM=\angle BAN+\angle DCM=90^{\circ}$。
图3:
$\because \odot O$是正五边形$ABCDE$的外接圆,点$M$,$N$分别从点$B$,$C$开始以相同的速度在$\odot O$上逆时针运动,
$\therefore \stackrel\frown{BM}=\stackrel\frown{CN}$,
$\therefore \stackrel\frown{CM}=\stackrel\frown{BN}$,
$\therefore CM=BN$,
又$\because AB=AE$,$\angle ABC=\angle E=108^{\circ}$,$\angle ACM=\angle ABN$,
$\therefore \triangle ACM\cong\triangle ABN(SAS)$,
$\therefore \angle CAM=\angle ABN$,
$\therefore \angle APN=\angle ABN+\angle BAP=\angle CAM+\angle BAP=\angle BAE=108^{\circ}$。
故答案为$60^{\circ}$;$90^{\circ}$;$108^{\circ}$。
(2)$\angle APN$的度数与正多边形边数$n$的关系是$\angle APN=\frac{(n-2)× 180^{\circ}}{n}$。
查看更多完整答案,请扫码查看


