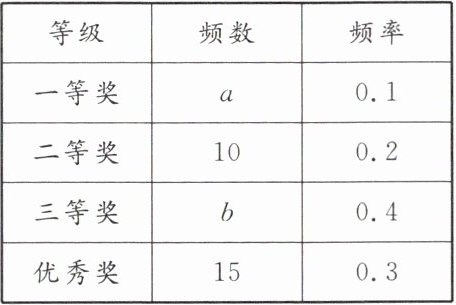
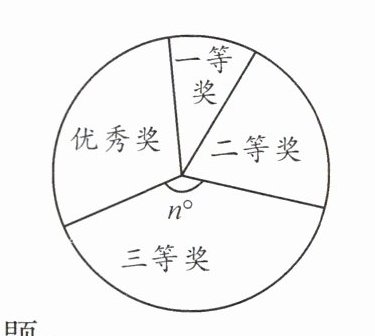
【例2】 某中学在全校学生中开展了以"保护环境"为主题的征文比赛,评选出一、二、三等奖和优秀奖.小明同学根据获奖结果,绘制成如图所示的统计表和扇形统计图.
请你根据以上图表提供的信息,解答下列问题:
(1)$a= $
(2)学校决定在获得一等奖的学生中,随机推荐两名学生代表学校参加市级比赛,其中王梦、李刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这两人的概率.
【考点】 列表法与画树状图法、频数(率)分布表、扇形统计图.
【专题】 图表型.
【分析】 (1)首先利用频数、频率之间的关系求得参赛人数,然后乘以一等奖的频率即可求得a值,乘以三等奖的频率即可求得b值,用三等奖的频率乘以$360°$即可求得n值.
(2)列表后即可将所有情况全部列举出来,从而求得恰好抽中这两人的概率.
解:(1)观察统计表知,二等奖的有10人,频率为0.2,故参赛的总人数为10÷0.2= 50,$a= 50×0.1= 5$,$b= 50×0.4= 20$,$n°=0.4×360°=144°$.
故答案为5,20,144.
(2)列表如下:
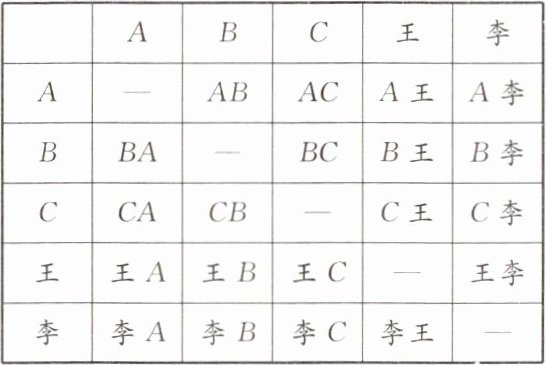
由表可知共有20种可能的情况,恰好是王梦、李刚的有2种情况,
∴恰好选中王梦和李刚两位同学的概率$P= \frac{2}{20}= \frac{1}{10}$.
【评析】 本题考查的是统计表和扇形统计图及概率的综合运用,读懂统计图表,从不同的统计图中得到必要的信息是解决问题的关键.
(2)设另外三名一等奖学生为$A$,$B$,$C$。列表如下:
| | $A$ | $B$ | $C$ | 王 | 李 |
| --- | --- | --- | --- | --- | --- |
| $A$ | — | $AB$ | $AC$ | $A$王 | $A$李 |
| $B$ | $BA$ | — | $BC$ | $B$王 | $B$李 |
| $C$ | $CA$ | $CB$ | — | $C$王 | $C$李 |
| 王 | 王$A$ | 王$B$ | 王$C$ | — | 王李 |
| 李 | 李$A$ | 李$B$ | 李$C$ | 李王 | — |
由表可知,共有20种等可能的情况,恰好是王梦、李刚的有2种情况,恰好选中王梦和李刚两位同学的概率 $P = \frac{2}{20} = \frac{1}{10}$。

请你根据以上图表提供的信息,解答下列问题:

(1)$a= $
5
, $b= $20
, $n= $144
.(2)学校决定在获得一等奖的学生中,随机推荐两名学生代表学校参加市级比赛,其中王梦、李刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这两人的概率.
【考点】 列表法与画树状图法、频数(率)分布表、扇形统计图.
【专题】 图表型.
【分析】 (1)首先利用频数、频率之间的关系求得参赛人数,然后乘以一等奖的频率即可求得a值,乘以三等奖的频率即可求得b值,用三等奖的频率乘以$360°$即可求得n值.
(2)列表后即可将所有情况全部列举出来,从而求得恰好抽中这两人的概率.
解:(1)观察统计表知,二等奖的有10人,频率为0.2,故参赛的总人数为10÷0.2= 50,$a= 50×0.1= 5$,$b= 50×0.4= 20$,$n°=0.4×360°=144°$.
故答案为5,20,144.
(2)列表如下:

由表可知共有20种可能的情况,恰好是王梦、李刚的有2种情况,
∴恰好选中王梦和李刚两位同学的概率$P= \frac{2}{20}= \frac{1}{10}$.
【评析】 本题考查的是统计表和扇形统计图及概率的综合运用,读懂统计图表,从不同的统计图中得到必要的信息是解决问题的关键.
(2)设另外三名一等奖学生为$A$,$B$,$C$。列表如下:
| | $A$ | $B$ | $C$ | 王 | 李 |
| --- | --- | --- | --- | --- | --- |
| $A$ | — | $AB$ | $AC$ | $A$王 | $A$李 |
| $B$ | $BA$ | — | $BC$ | $B$王 | $B$李 |
| $C$ | $CA$ | $CB$ | — | $C$王 | $C$李 |
| 王 | 王$A$ | 王$B$ | 王$C$ | — | 王李 |
| 李 | 李$A$ | 李$B$ | 李$C$ | 李王 | — |
由表可知,共有20种等可能的情况,恰好是王梦、李刚的有2种情况,恰好选中王梦和李刚两位同学的概率 $P = \frac{2}{20} = \frac{1}{10}$。
答案:
(1)参赛总人数:$10 ÷ 0.2 = 50$(人)。
$a = 50 × 0.1 = 5$。
$b = 50 × 0.4 = 20$。
$n = 0.4 × 360^\circ = 144^\circ$。
答案为:5;20;144。
(2)设另外三名一等奖学生为$A$,$B$,$C$。
列表如下:
| | $A$ | $B$ | $C$ | 王 | 李 |
| --- | --- | --- | --- | --- | --- |
| $A$ | — | $AB$ | $AC$ | $A$王 | $A$李 |
| $B$ | $BA$ | — | $BC$ | $B$王 | $B$李 |
| $C$ | $CA$ | $CB$ | — | $C$王 | $C$李 |
| 王 | 王$A$ | 王$B$ | 王$C$ | — | 王李 |
| 李 | 李$A$ | 李$B$ | 李$C$ | 李王 | — |
由表可知,共有20种等可能的情况,恰好是王梦、李刚的有2种情况,
恰好选中王梦和李刚两位同学的概率 $P = \frac{2}{20} = \frac{1}{10}$。
$a = 50 × 0.1 = 5$。
$b = 50 × 0.4 = 20$。
$n = 0.4 × 360^\circ = 144^\circ$。
答案为:5;20;144。
(2)设另外三名一等奖学生为$A$,$B$,$C$。
列表如下:
| | $A$ | $B$ | $C$ | 王 | 李 |
| --- | --- | --- | --- | --- | --- |
| $A$ | — | $AB$ | $AC$ | $A$王 | $A$李 |
| $B$ | $BA$ | — | $BC$ | $B$王 | $B$李 |
| $C$ | $CA$ | $CB$ | — | $C$王 | $C$李 |
| 王 | 王$A$ | 王$B$ | 王$C$ | — | 王李 |
| 李 | 李$A$ | 李$B$ | 李$C$ | 李王 | — |
由表可知,共有20种等可能的情况,恰好是王梦、李刚的有2种情况,
恰好选中王梦和李刚两位同学的概率 $P = \frac{2}{20} = \frac{1}{10}$。
查看更多完整答案,请扫码查看


