1. 一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下列函数关系式:$h= -5(t-1)^{2}+7$,则小球距离地面的最大高度是(
A.1米
B.6米
C.7米
D.8米
C
)A.1米
B.6米
C.7米
D.8米
答案:
C
2. 某商店销售一种帽子,若这种帽子每天获利y(元)与销售单价x(元)满足关系$y= -x^{2}+70x-800$,要想获得最大利润,则销售单价为(
A.30元
B.35元
C.40元
D.45元
B
)A.30元
B.35元
C.40元
D.45元
答案:
B
3. 如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,则拱门的最大高度为

200
.
答案:
200
4. 如图,$AC⊥CD$,甲、乙两船分别从A地和C地同时开出,各沿箭头所指方向航行,AC两地相距10海里,甲、乙两船的速度分别是16海里/时和12海里/时,多长时间后两船相距最近?最近距离是多少?
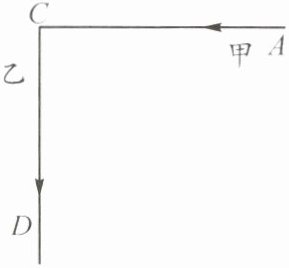

答案:
设经过$ t $小时后两船相距最近。
此时甲船航行的路程为$ 16t $海里,乙船航行的路程为$ 12t $海里。
根据题意,两船航行方向互相垂直,由勾股定理得两船距离$ d $的平方为:
$ d^2=(10 - 16t)^2 + (12t)^2 $
展开并整理得:
$ d^2=100 - 320t + 256t^2 + 144t^2=400t^2 - 320t + 100 $
对于二次函数$ d^2=400t^2 - 320t + 100 $,$ a=400>0 $,当$ t=-\frac{b}{2a}=\frac{320}{2×400}=0.4 $时,$ d^2 $取最小值。
将$ t=0.4 $代入$ d^2 $得:
$ d^2=400×(0.4)^2 - 320×0.4 + 100=64 - 128 + 100=36 $
则$ d=\sqrt{36}=6 $
0.4小时后两船相距最近,最近距离是6海里。
此时甲船航行的路程为$ 16t $海里,乙船航行的路程为$ 12t $海里。
根据题意,两船航行方向互相垂直,由勾股定理得两船距离$ d $的平方为:
$ d^2=(10 - 16t)^2 + (12t)^2 $
展开并整理得:
$ d^2=100 - 320t + 256t^2 + 144t^2=400t^2 - 320t + 100 $
对于二次函数$ d^2=400t^2 - 320t + 100 $,$ a=400>0 $,当$ t=-\frac{b}{2a}=\frac{320}{2×400}=0.4 $时,$ d^2 $取最小值。
将$ t=0.4 $代入$ d^2 $得:
$ d^2=400×(0.4)^2 - 320×0.4 + 100=64 - 128 + 100=36 $
则$ d=\sqrt{36}=6 $
0.4小时后两船相距最近,最近距离是6海里。
查看更多完整答案,请扫码查看


