《2025年新课标学习方法指导丛书九年级数学上册浙教版》

【例1】已知二次函数$y= \frac{1}{2}x^{2}-x-\frac{3}{2}$.
(1)求抛物线的开口方向、对称轴和顶点M的坐标.
(2)设抛物线与y轴交于点C,与x轴交于A,B两点,求点C,A,B的坐标.
(3)画出函数图象的示意图.
(4)求$\triangle MAB$的周长和面积.
(5)当x为何值时,y随着x的增大而减小？当x为何值时,y有最大(小)值,这个最大(小)值是多少？
(6)当x为何值时,$y＜0$？当x为何值时,$y＞0$？

答案：
解：
(1)$\because a= \frac{1}{2}＞0$,$\therefore$抛物线的开口向上.
$\because y= \frac{1}{2}x^{2}-x-\frac{3}{2}= \frac{1}{2}(x-1)^{2}-2$,
$\therefore对称轴为直线x= 1$,顶点M的坐标为$(1,-2)$.
(2)由$x= 0$,得$y= -\frac{3}{2}$,
$\therefore$抛物线与y轴的交点为$C(0,-\frac{3}{2})$,
由$y= 0$,得$0= \frac{1}{2}x^{2}-x-\frac{3}{2}$,
解得$x_{1}= -1$,$x_{2}= 3$.
$\therefore$抛物线与x轴的交点为$A(-1,0)$,$B(3,0)$.
(3)示意图如图所示,画法略.

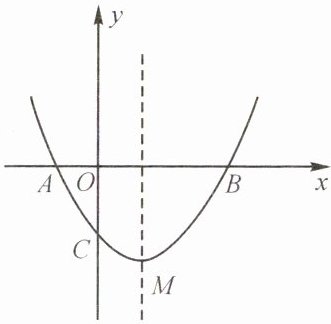
(4)连结MA,MB(图略),由对称性可知$MA= MB= \sqrt{2^{2}+2^{2}}= \sqrt{8}= 2\sqrt{2}$,$AB= |x_{1}-x_{2}|= 4$,
$\therefore\triangle MAB的周长= 2MA+AB= 2\sqrt{2}×2 + 4= 4\sqrt{2}+4$,
$\triangle MAB的面积= \frac{1}{2}×4×2= 4$.
(5)当$x\leq1$时,y随着x的增大而减小；
当$x= 1$时,y有最小值,$y_{min}= -2$.
(6)由图象可知,
当$-1＜x＜3$时,$y＜0$；当$x＜-1或x＞3$时,$y＞0$.