《2025年新课标学习方法指导丛书九年级数学上册浙教版》

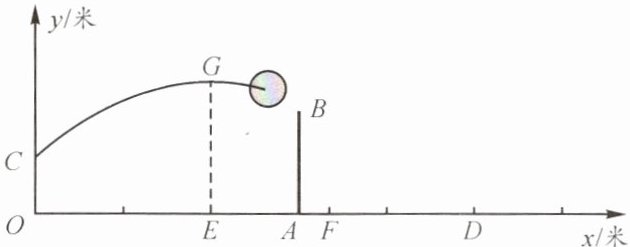
10. 如图,已知排球场的长度OD为15米,位于排球场中线处球网的高度AB为2.5米,一队员站在点O处发球,排球从点O的正上方2米的C点向正前方飞出,当排球运行至离点O的水平距离OE为5米时,到达最高点G,建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为3米时,求排球飞行的高度y(米)关于水平距离x(米)的函数表达式.(不要求写自变量x的取值范围)
(2)在第(1)题的条件下,对方在距球网0.5米的点F处有一队员,她起跳后的最大高度为2.7米,这次她是否可以拦网成功？请通过计算说明.

答案：
(1) 由题意知，排球飞行轨迹为抛物线，顶点G的坐标为(5, 3)，设函数表达式为$y=a(x-5)^2+3$。
将点$C(0,2)$代入，得：
$2=a(0-5)^2+3$
$2=25a+3$
$25a=-1$
$a=-\frac{1}{25}$
故函数表达式为$y=-\frac{1}{25}(x-5)^2+3$。
(2) 球网在中线处，$OA=\frac{15}{2}=7.5$米，点$F$距球网0.5米，$x=7.5+0.5=8$。
当$x=8$时，
$y=-\frac{1}{25}(8-5)^2+3=-\frac{9}{25}+3=2.64$。
因为$2.64＜2.7$，所以可以拦网成功。

11. 施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以点O为原点,OM所在直线为x轴建立直角坐标系(如图所示).
(1)直接写出点M及抛物线顶点P的坐标.
(2)求出这条抛物线的函数表达式.
(3)施工队计划在隧道门口搭建一个矩形"脚手架"CDAB,使点A,D在抛物线上,点B,C在地面OM上.为了筹备材料,需求出"脚手架"三根木杆AB,AD,DC的长度之和的最大值.请你帮施工队计算一下.

答案：
(1)M(12,0)，P(6,6)。
(2)设抛物线的函数表达式为$y = a(x - 6)^{2}+6$，把(0,0)代入得：
$0=a(0 - 6)^{2}+6$
$0 = 36a+6$
$36a=-6$
解得$a=-\frac{1}{6}$
所以抛物线的函数表达式为$y = -\frac{1}{6}(x - 6)^{2}+6=-\frac{1}{6}x^{2}+2x$。
(3)设$A(x,y)$，因为四边形$ABCD$是矩形，所以$AB = DC = y$，$BC = AD = 2(6 - x)$，$y = -\frac{1}{6}x^{2}+2x$。
设$l = AB + AD + DC$，则
$l = 2y + 2(6 - x)=2(-\frac{1}{6}x^{2}+2x)+12 - 2x=-\frac{1}{3}x^{2}+2x + 12=-\frac{1}{3}(x - 3)^{2}+15$。
因为$-\frac{1}{3}＜0$，所以当$x = 3$时，$l$有最大值$15$。
即三根木杆长度之和的最大值为$15$米。