第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
学习任务一 切线的判定定理
如图 24.2.2 - 10①,点 $ A $ 是 $ \odot O $ 上任意一点。
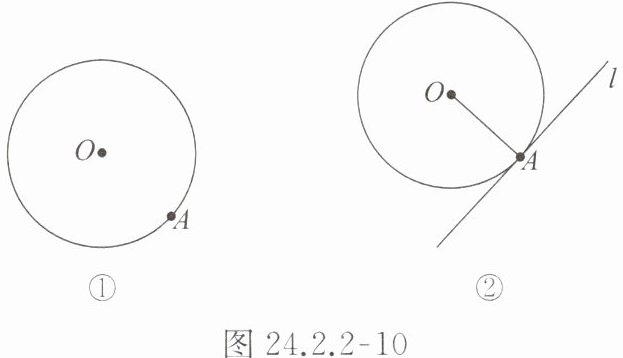
经过半径 $ OA $ 的外端点 $ A $ 作直线 $ l \perp OA $(如图 24.2.2 - 10②),则圆心 $ O $ 到直线 $ l $ 的距离是多少?直线 $ l $ 和 $ \odot O $ 有什么位置关系?为什么?
归纳
如图 24.2.2 - 10①,点 $ A $ 是 $ \odot O $ 上任意一点。

经过半径 $ OA $ 的外端点 $ A $ 作直线 $ l \perp OA $(如图 24.2.2 - 10②),则圆心 $ O $ 到直线 $ l $ 的距离是多少?直线 $ l $ 和 $ \odot O $ 有什么位置关系?为什么?
归纳
答案:
圆心O到直线l的距离是OA的长,直线l与⊙O相切,因为圆心O到直线l的距离等于半径OA.
圆的切线的判定定理:
经过半径的
经过半径的
外端
并且垂直于
这条半径的直线是圆的切线。
答案:
外端 垂直于
学习任务二 切线的性质定理
如图 24.2.2 - 11,直线 $ l $ 是 $ \odot O $ 的切线,切点为 $ A $,则 $ l $ 与 $ OA $ 的位置关系是
理由:假设 $ l $ 与 $ OA $
图 24.2.2 - 11
图 24.2.2 - 12

归纳
如图 24.2.2 - 11,直线 $ l $ 是 $ \odot O $ 的切线,切点为 $ A $,则 $ l $ 与 $ OA $ 的位置关系是
l⊥OA
。理由:假设 $ l $ 与 $ OA $
不垂直
,如图 24.2.2 - 12,过点 $ O $ 作 $ OB \perp l $ 于点 $ B $,则在 $ Rt \triangle OAB $ 中,$ OB $ 与 $ OA $ 的大小关系是 $ OB $ <
$ OA $,即圆心 $ O $ 到直线 $ l $ 的距离 $ OB $ 小于
半径(填“大于”“小于”或“等于”),则 $ l $ 与 $ \odot O $ 的位置关系是相交
,与 $ l $ 是 $ \odot O $ 的切线矛盾,所以假设不成立,所以 $ l $ ⊥
$ OA $。图 24.2.2 - 11
图 24.2.2 - 12

归纳
答案:
l⊥OA 不垂直 < 小于 相交 ⊥
切线的性质定理:圆的切线
垂直于
过切点的半径。
答案:
垂直于
1. 如图 24.2.2 - 13,$ \triangle ABC $ 的一边 $ AB $ 是 $ \odot O $ 的直径,请你添加一个条件,使 $ BC $ 是 $ \odot O $ 的切线,你所添加的条件为

AB⊥BC(答案不唯一)
。
答案:
AB⊥BC(答案不唯一)
2. 如图 24.2.2 - 14,直线 $ l $ 与 $ \odot O $ 相切于点 $ B $,点 $ A $ 在直线 $ l $ 上,$ OA = 10 $,$ \angle OAB = 30^{\circ} $,则 $ \odot O $ 的半径为
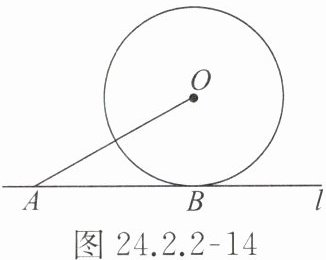
5
。
答案:
5
【例 1】(湖北黄冈中考节选)已知:如图 24.2.2 - 15,$ MN $ 为 $ \odot O $ 的直径,$ ME $ 是 $ \odot O $ 的弦,$ MD $ 垂直于过点 $ E $ 的直线 $ DE $,垂足为点 $ D $,且 $ ME $ 平分 $ \angle DMN $。
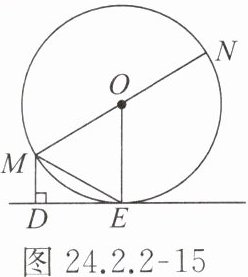
求证:$ DE $ 是 $ \odot O $ 的切线。
思考 1:因为 $ DE $ 与 $ \odot O $ 有公共点 $ E $,所以要证明 $ DE $ 是 $ \odot O $ 的切线,只需证明
思考 2:因为已知 $ MD \perp DE $,所以可把证明直线与 $ \odot O $ 相切转化为证明 $ MD // $

证明:
(一题多解)请尝试用其他方法证明。

求证:$ DE $ 是 $ \odot O $ 的切线。
思考 1:因为 $ DE $ 与 $ \odot O $ 有公共点 $ E $,所以要证明 $ DE $ 是 $ \odot O $ 的切线,只需证明
OE⊥DE
。思考 2:因为已知 $ MD \perp DE $,所以可把证明直线与 $ \odot O $ 相切转化为证明 $ MD // $
OE
。
证明:
因为OM=OE,所以∠OME=∠OEM.
因为ME平分∠DMN,所以∠OME=∠DME,
所以∠OEM=∠DME,所以MD//OE.
因为MD⊥DE,所以OE⊥DE.
又因为OE为⊙O的半径,所以DE是⊙O的切线.
因为ME平分∠DMN,所以∠OME=∠DME,
所以∠OEM=∠DME,所以MD//OE.
因为MD⊥DE,所以OE⊥DE.
又因为OE为⊙O的半径,所以DE是⊙O的切线.
(一题多解)请尝试用其他方法证明。
证明:如答图24.2.2-2,连接NE.
因为MN是⊙O的直径,
所以∠MEN=∠1+∠2=90°.
因为OM=OE,
所以∠1=∠4,
所以∠4+∠2=90°.
因为MD⊥DE,所以∠5+∠3=90°.
因为ME平分∠DMN,所以∠4=∠5,
所以∠2=∠3,所以∠1+∠3=90°,
即OE⊥DE.因为OE是⊙O的半径,所以DE是⊙O的切线.
因为MN是⊙O的直径,
所以∠MEN=∠1+∠2=90°.
因为OM=OE,
所以∠1=∠4,
所以∠4+∠2=90°.
因为MD⊥DE,所以∠5+∠3=90°.
因为ME平分∠DMN,所以∠4=∠5,
所以∠2=∠3,所以∠1+∠3=90°,
即OE⊥DE.因为OE是⊙O的半径,所以DE是⊙O的切线.
答案:
思考1:OE⊥DE
思考2:OE
证明:因为OM=OE,所以∠OME=∠OEM.
因为ME平分∠DMN,所以∠OME=∠DME,
所以∠OEM=∠DME,所以MD//OE.
因为MD⊥DE,所以OE⊥DE.
又因为OE为⊙O的半径,所以DE是⊙O的切线.
[一题多解]
证明:如答图24.2.2-2,连接NE.
因为MN是⊙O的直径,
所以∠MEN=∠1+∠2=90°.
因为OM=OE,
所以∠1=∠4,
所以∠4+∠2=90°.
因为MD⊥DE,所以∠5+∠3=90°.
因为ME平分∠DMN,所以∠4=∠5,
所以∠2=∠3,所以∠1+∠3=90°,
即OE⊥DE.因为OE是⊙O的半径,所以DE是⊙O的切线.
思考2:OE
证明:因为OM=OE,所以∠OME=∠OEM.
因为ME平分∠DMN,所以∠OME=∠DME,
所以∠OEM=∠DME,所以MD//OE.
因为MD⊥DE,所以OE⊥DE.
又因为OE为⊙O的半径,所以DE是⊙O的切线.
[一题多解]
证明:如答图24.2.2-2,连接NE.
因为MN是⊙O的直径,
所以∠MEN=∠1+∠2=90°.
因为OM=OE,
所以∠1=∠4,
所以∠4+∠2=90°.
因为MD⊥DE,所以∠5+∠3=90°.
因为ME平分∠DMN,所以∠4=∠5,
所以∠2=∠3,所以∠1+∠3=90°,
即OE⊥DE.因为OE是⊙O的半径,所以DE是⊙O的切线.
查看更多完整答案,请扫码查看


