《2025年人教金学典同步解析与测评九年级数学上册人教版云南专版》

1. 当a为何实数时,方程$(a + √2)x^{a^2} - 2x + 1 = 0$是关于x的一元二次方程？

答案： a=√2

【例2】将下列方程化成一元二次方程的一般形式,并写出其中的二次项系数、一次项系数及常数项。
(1)3x^2 = 4x；(2)2y^2 = 3y - 4；
(3)(2x - 2)^2 = 8(x + 2)；(4)$\frac{x^2}{3} - \frac{x + 1}{2} = 1$。
解：

答案：
(1)移项，得一元二次方程的一般形式为3x²-4x=0.其中二次项系数为3，一次项系数为-4，常数项为0.
(2)移项，得一元二次方程的一般形式为2y²-3y+4=0. 其中二次项系数为2，一次项系数为-3，常数项为4.
(3)去括号，得4x²-8x+4=8x+16.移项、合并同类项、系数化为1，得一元二次方程的一般形式为x²-4x-3=0. 其中二次项系数为1，一次项系数为-4，常数项为-3.
(4)去分母，得2x²-3(x+1)=6.去括号、移项、合并同类项，得一元二次方程的一般形式为2x²-3x-9=0. 其中二次项系数为2，一次项系数为-3，常数项为-9.

2. 方程$2x^2 = 6x + 9$的二次项系数、一次项系数、常数项分别为(C)
A.6,2,9
B.2,-6,9
C.2,-6,-9
D.-2,6,9

答案： C

【例3】(山东菏泽中考)已知m是关于x的方程$x^2 - 2x - 3 = 0$的一个根,则$2m^2 - 4m = $6。

答案： 6

3. (黑龙江龙东中考)已知2 + √3是关于x的一元二次方程$x^2 - 4x + m = 0$的一个实数根,则实数m的值是(B)
A.0
B.1
C.-3
D.-1

答案： B

【例4】某超市销售一种品牌童装,平均每天可售出50件,每件盈利40元。为了加快投资资金回笼,超市采用降价措施,每件童装每降价2元,平均每天就多售出8件。如果平均每天销售童装利润为1000元,那么每件童装应降价多少元？(只需列出方程,并化为一般形式,不必求解)
解：

答案： 设每件童装应降价x元. 根据题意，得(50+（x/2）×8)(40-x)=1000. 整理，得2x²-55x-500=0.

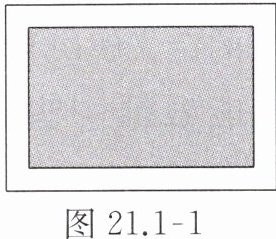
4. 在一幅长为80 cm、宽为50 cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图21.1 - 1(示意图)所示。如果整个挂图的面积是$5400 cm^2,$设金色纸边的宽为x cm,那么x满足的方程是(B)

$A. 2x^2 + 125x - 900 = 0$
$B. x^2 + 65x - 350 = 0$
$C. 2x^2 + 125x + 900 = 0$
$D. x^2 - 65x - 350 = 0$

答案： B

1. 下列各选项中是一元二次方程的是(C)
$A.x^2 + 1 = x(x + 1)$
$B.x^2 - 2x - 3$
$C.x^2 - 1 = 0$
D.$\frac{1}{x} + x^2 = 1$

答案： C

2. 已知m是方程$x^2 - x - 1 = 0$的一个根,则代数式$m^2 - m + 1$的值等于(D)
A.-1
B.0
C.1
D.2

答案： D

3. 关于x的方程$(m^2 - 4)x^2 - (m - 2)x - 1 = 0,$当m≠±2时,是一元二次方程；当m=-2时,是一元一次方程。

答案： ≠±2 =-2

4. 某住宅小区准备在每两幢楼房之间开辟一块面积为$300 m^2$的长方形绿地,并且长比宽多12 m,设长方形绿地的宽为x m,则可列方程为x(x+12)=300；把所列方程化成一般形式为x²+12x-300=0,其二次项系数为1,一次项系数为12,常数项为-300。

答案： x(x+12)=300 x²+12x-300=0 1 12 -300