《2025年人教金学典同步解析与测评九年级数学上册人教版云南专版》

3. 已知抛物线 $ y = ax^2 (a \neq 0) $ 经过点 $ A(-2, -8) $。求此抛物线对应的函数解析式,并写出该抛物线的开口方向、对称轴和顶点坐标。

答案： 解:
(1)抛物线对应的函数解析式为 $ y=-2x^{2} $.
抛物线 $ y=-2x^{2} $ 开口向下,对称轴是 y 轴,顶点坐标是(0,0).

1. 已知 $ y = (k - 1)x^{k^2 - 2} $ 是关于 $ x $ 的二次函数,且有最大值,则 $ k = $(A)
A.$-2$
B.$2$
C.$3$
D.$-3$

答案： A

2. 如图22.1.2-4,$ A $,$ B $ 为抛物线 $ y = ax^2 $ 上的两点,且 $ AB \perp y $ 轴于点 $ (0, 6) $。若 $ AB = 6 $,则该抛物线对应的函数解析式为 $ y=\frac{2}{3}x^{2} $。

答案： $ y=\frac{2}{3}x^{2} $

3. 若抛物线 $ y = ax^2 $ 与直线 $ y = 2x - 3 $ 交于点 $ P(1, b) $,则 $ a = $-1,$ b = $-1。

答案： -1 -1

4. 如图22.1.2-5,直线 $ l $ 过 $ A(3, 0) $ 和 $ B(0, 3) $ 两点,它与二次函数 $ y = ax^2 $ 的图象在第一象限内交于点 $ P $,若 $ \triangle AOP $ 的面积为3,求该二次函数的解析式。

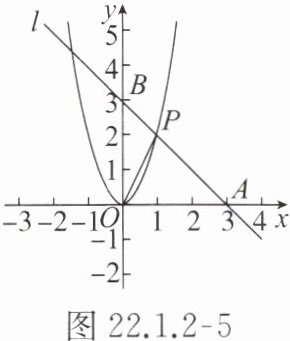
答案： 解:二次函数的解析式为 $ y=2x^{2} $.

5. 若二次函数 $ y = mx^2 $ 的图象经过点 $ A(x_1, y_1) $ 和点 $ B(x_2, y_2) $,当 $ x_1 ＜ x_2 ＜ 0 $ 时,$ y_1 ＞ y_2 $,则 $ m $ 的取值范围是 $ m＞0 $。

答案： $ m＞0 $

6. 某地一座抛物线形拱桥的示意图如图22.1.2-6所示,桥拱在竖直平面内,与水平桥面相交于 $ A $,$ B $ 两点,桥拱最高点 $ C $ 到 $ AB $ 的距离为9 m,$ AB = 36 $ m,$ D $,$ E $ 为桥拱底部的两点,且 $ DE // AB $,点 $ E $ 到直线 $ AB $ 的距离为7 m,求 $ DE $ 的长。

答案： 解:$ DE=48 $ m.

7. 问题：如图22.1.2-7,在 $ x $ 轴上有两点 $ A(m, 0) $,$ B(n, 0) (n ＞ m ＞ 0) $。分别过点 $ A $,$ B $ 作 $ x $ 轴的垂线,交抛物线 $ y = x^2 $ 于点 $ C $,$ D $,直线 $ OC $ 交直线 $ BD $ 于点 $ E $,直线 $ OD $ 交直线 $ AC $ 于点 $ F $,点 $ E $,$ F $ 的纵坐标分别记为 $ y_E $,$ y_F $。探究：当 $ m = 1 $,$ n = 2 $ 时,$ y_E = $ ______,$ y_F = $ ______；当 $ m = 3 $,$ n = 5 $ 时,$ y_E = $ ______,$ y_F = $ ______；归纳：对任意 $ m $,$ n (n ＞ m ＞ 0) $,猜想 $ y_E $ 与 $ y_F $ 的大小关系,并证明你的猜想。应用：(1) 若将“抛物线 $ y = x^2 $”改为“抛物线 $ y = ax^2 (a ＞ 0) $”,其他条件不变,请直接写出 $ y_E $ 与 $ y_F $ 的大小关系；(2) 连接 $ EF $,$ AE $,当 $ S_{四边形 OFEB} = 3S_{\triangle OFE} $ 时,求出 $ m $ 与 $ n $ 的数量关系并说明四边形 $ OFEA $ 的形状。

【探究】2 2 15 15
【归纳】解:猜想:$ y_{E}=y_{F} $.证明:略.
【应用】解:
(1)$ y_{E}=y_{F} $.
(2)$ n=2m $.四边形 OFEA 是平行四边形.

答案： 【探究】2 2 15 15
【归纳】解:猜想:$ y_{E}=y_{F} $.证明:略.
【应用】解:
(1)$ y_{E}=y_{F} $.
(2)$ n=2m $.四边形 OFEA 是平行四边形.