《2025年人教金学典同步解析与测评九年级数学上册人教版云南专版》

学习任务一 圆的旋转不变性及圆心角的概念
1. 圆的旋转不变性
圆具有旋转不变性,它绕圆心旋转任意一个角度都能与它本身重合,同时圆也是中心对称图形,圆心是对称中心.

答案： 本身 圆心

2. 圆心角

顶点在圆心的角,如图24.1.3 - 1所示,∠AOB是圆心角.
学习任务二 弧、弦、圆心角的关系

答案： 圆心 弧 弦 $\overset{\frown}{AB}$ $\overset{\frown}{CD}$ AB CD 圆心角 弦 $\angle AOB$ $\angle COD$ AB CD 圆心角 优弧 劣弧 $\angle AOB$ $\angle COD$ $\overset{\frown}{AB}$ $\overset{\frown}{CD}$ $\overset{\frown}{ACB}$ $\overset{\frown}{CBD}$

归纳
在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.

答案： 圆心角 弧 弦

1. 下列图形中表示的角是圆心角的是 (A)

答案： A

2. 如图24.1.3 - 2,在⊙O中,⌢AB = ⌢AC,∠AOB = 122°,则∠AOC的度数为 (A)

A.122°
B.120°
C.61°
D.58°

答案： A

3. 已知⊙O的半径为5 cm,弦AB的长为5 cm,则弦AB所对的圆心角∠AOB = $60^{\circ }$.

答案： $60^{\circ }$

【例1】 下列说法正确吗？
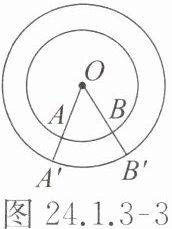
如图24.1.3 - 3,小明说：“因为⌢AB和⌢A′B′所对的圆心角都是∠O,所以⌢AB = ⌢A′B′.”
如图24.1.3 - 4,小华说：“因为AB = CD,所以AB所对的⌢AB等于CD所对的⌢CAD.”


解：

答案： 小明的说法不正确.因为只有在同圆或等圆中,相等的圆心角所对的弧才相等.小华的说法不正确,$\overset{\frown}{AB}$是劣弧,$\overset{\frown}{CAD}$是优弧,显然不相等,在题图中,若$AB=CD$,则$\overset{\frown}{AB}=\overset{\frown}{CD}$,$\overset{\frown}{CAD}=\overset{\frown}{ACB}$.