《2025年学典四川八年级数学上册北师大版》

9. 一盘蚊香长 $ 50cm $,点燃时每小时缩短 $ 5cm $。
(1)请写出点燃后蚊香的长 $ y $(单位：$ cm $)与蚊香燃烧时间 $ t $(单位：$ h $)之间的函数关系式,并判断 $ y $ 是否是 $ t $ 的一次函数；
(2)该蚊香可燃烧多长时间？

答案：
(1) 由题意得，蚊香每小时缩短5cm，燃烧t小时后缩短5t cm，初始长度为50cm，所以函数关系式为：$y = 50 - 5t$。因为该函数符合一次函数$y = kt + b$（$k$、$b$为常数，$k \neq 0$）的形式，其中$k = -5$，$b = 50$，所以$y$是$t$的一次函数。
(2) 当蚊香燃尽时，$y = 0$，即$50 - 5t = 0$，解得$t = 10$。所以该蚊香可燃烧10小时。

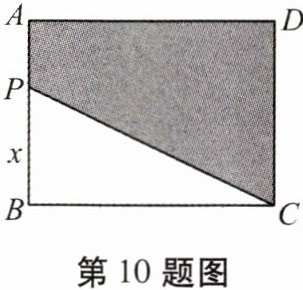
10. 如图,在长方形 $ ABCD $ 中,$ AB = 6 $,$ BC = 8 $,点 $ P $ 在边 $ AB $ 上运动,设 $ PB = x $,图中阴影部分的面积为 $ y $。
(1)写出 $ y $ 与 $ x $ 之间的关系式；
(2)当 $ x $ 的值为 $ 5 $ 时,阴影部分的面积为多少？

答案：
(1) $y=-4x + 48$；
(2) $28$。

11. $[a, b]$ 为一次函数 $ y = ax + b (a \neq 0, a, b $ 为常数)的“关联数”。若“关联数”是 $[1, m - \sqrt{2}]$ 的一次函数是正比例函数,则关于 $ x $ 的方程 $ x + \frac{1}{m} = \sqrt{2} $ 的解为$x = \frac{\sqrt{2}}{2}$。

答案： $x = \frac{\sqrt{2}}{2}$（或写为$x=\frac{1}{\sqrt{2}}$的等价形式，但按题目要求填最简形式）

12. 已知 $ y - 2 $ 与 $ x + 1 $ 成正比例,且当 $ x = -2 $ 时,$ y = 5 $。
(1)求 $ y $ 与 $ x $ 之间的函数关系式；
(2)当 $ x = -3 $ 时,求 $ y $ 的值。

答案：
(1)
因为$y - 2$与$x + 1$成正比例，所以设$y - 2=k(x + 1)$。
把$x = - 2$，$y = 5$代入$y - 2=k(x + 1)$得：
$5 - 2=k(-2 + 1)$，
即$3 = - k$，解得$k=-3$。
把$k = - 3$代入$y - 2=k(x + 1)$得$y - 2=-3(x + 1)$，
$y-2=-3x-3$，
$y=-3x - 1$。
(2)
当$x = - 3$时，$y=-3×(-3)-1$，
$y = 9 - 1=8$。
综上，答案为：
(1)$y=-3x - 1$；
(2)8。

13. 工艺品店销售某种工艺品,调查发现：当销售价为 $ 40 $ 元/件时,每天的销售量为 $ 20 $ 件；当销售价每降低 $ 1 $ 元,每天的销售量就多 $ 5 $ 件。设销售价为 $ x $ 元/件,每天的销售量为 $ y $ 件。
(1)求 $ y $ 与 $ x $ 之间的函数关系式；
(2)某天销售该工艺品,每件获得的利润为 $ 15 $ 元,若当天共盈利 $ 750 $ 元,求这天该种工艺品每件的销售价。

答案：
(1)由题意，销售价为$x$元/件时，销售价降低了$(40 - x)$元，销售量增加$5(40 - x)$件，故$y = 20 + 5(40 - x)$，化简得$y = -5x + 220$。
(2)每件利润为15元，总盈利750元，销售量为$750÷15 = 50$件。将$y = 50$代入$y = -5x + 220$，得$50 = -5x + 220$，解得$x = 34$。
(1)$y = -5x + 220$；
(2)34元。