第4页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
1. 在直角三角形中,若勾为 9,股为 12,则弦为 (
A.9
B.12
C.15
D.21
C
)A.9
B.12
C.15
D.21
答案:
C
2. 如图,为了测得湖两岸 A,B 两点之间的距离,一个观测者在点 C 设桩,使∠ABC = 90°,并测得 AC = 20 米,BC = 16 米,则点 A,B 之间的距离为 (
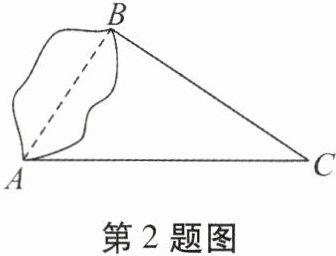
A.12 米
B.13 米
C.15 米
D.25 米
A
)
A.12 米
B.13 米
C.15 米
D.25 米
答案:
A
3. 我国是最早了解勾股定理的国家之一. 下列选项中,不能证明勾股定理的是 (
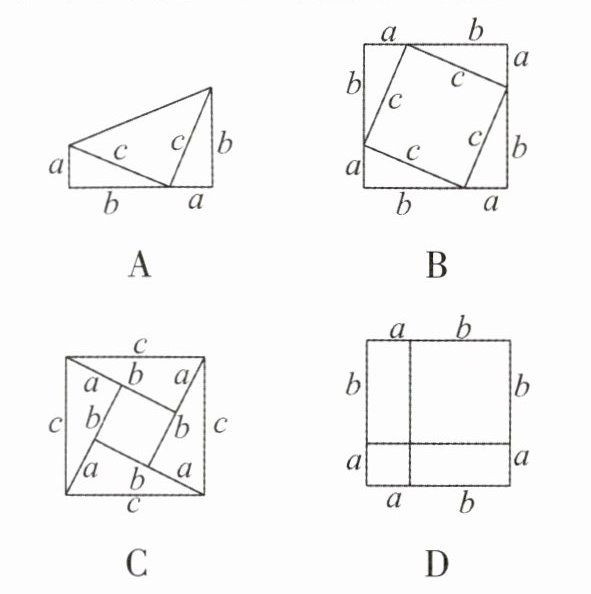
D
)
答案:
D
4. 已知一个直角三角形的两边长分别为 4 和 3,则它的斜边长为
5或4
.
答案:
5或4
5. 《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺. 问折高者几何? 意思是:一根竹子,原高 1 丈(1 丈 = 10 尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部 6 尺远,问折断处离地面的高度是多少? 设折断处离地面的高度为 x 尺,则可列方程为
$ x^2 + 6^2 = (10 - x)^2 $
.
答案:
$ x^2 + 6^2 = (10 - x)^2 $
6. 如图,在 Rt△ABC 中,∠C = 90°,AC = 12,边 BC 上的中线 AD 长为 13,求边 BC 的长.
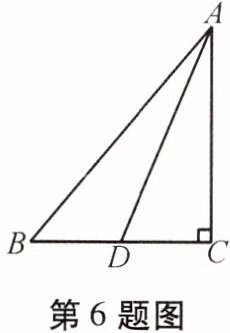

答案:
在$Rt \bigtriangleup ADC$中,
根据勾股定理,$AC^{2} + DC^{2} = AD^{2}$,
已知$AC = 12$,$AD = 13$,
则$DC = \sqrt{AD^{2} - AC^{2}} = \sqrt{13^{2} - 12^{2}} = \sqrt{169 - 144} = \sqrt{25} = 5$,
因为$AD$是$BC$边上的中线,
所以$BC = 2DC = 2 × 5 = 10$。
故答案为:$10$。
根据勾股定理,$AC^{2} + DC^{2} = AD^{2}$,
已知$AC = 12$,$AD = 13$,
则$DC = \sqrt{AD^{2} - AC^{2}} = \sqrt{13^{2} - 12^{2}} = \sqrt{169 - 144} = \sqrt{25} = 5$,
因为$AD$是$BC$边上的中线,
所以$BC = 2DC = 2 × 5 = 10$。
故答案为:$10$。
7. 如图是中国最早的一部数学著作——《周髀》中记载的赵爽弦图,是由四个全等的直角三角形拼成的图形. 我国古代数学家用它来证明勾股定理,请根据该图提供的信息证明勾股定理.
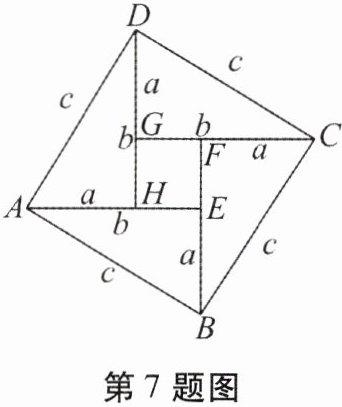

答案:
设大正方形的边长为$c$,四个全等的直角三角形的两条直角边分别为$a$和$b$,且$c$为斜边。
大正方形的面积为$c^{2}$。
中间小正方形的边长为$(b - a)$,所以小正方形的面积为$(b - a)^{2}$。
四个直角三角形的面积和为$4×\frac{1}{2}ab = 2ab$。
因为大正方形的面积等于四个直角三角形的面积与中间小正方形的面积之和,即$c^{2}=2ab+(b - a)^{2}$。
将$(b - a)^{2}$展开得$b^{2}-2ab + a^{2}$,代入上式可得:
$c^{2}=2ab + b^{2}-2ab + a^{2}$。
化简得$c^{2}=a^{2}+b^{2}$。
综上,证明了勾股定理,即直角三角形两直角边的平方和等于斜边的平方。
大正方形的面积为$c^{2}$。
中间小正方形的边长为$(b - a)$,所以小正方形的面积为$(b - a)^{2}$。
四个直角三角形的面积和为$4×\frac{1}{2}ab = 2ab$。
因为大正方形的面积等于四个直角三角形的面积与中间小正方形的面积之和,即$c^{2}=2ab+(b - a)^{2}$。
将$(b - a)^{2}$展开得$b^{2}-2ab + a^{2}$,代入上式可得:
$c^{2}=2ab + b^{2}-2ab + a^{2}$。
化简得$c^{2}=a^{2}+b^{2}$。
综上,证明了勾股定理,即直角三角形两直角边的平方和等于斜边的平方。
查看更多完整答案,请扫码查看


