《2025年学典四川八年级数学上册北师大版》

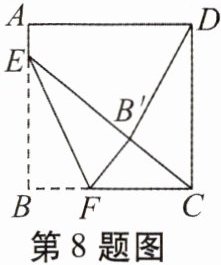
8. 如图,正方形$ABCD$的边长是8,点$E在边AB$上,$AE= \frac{3}{2}$,点$F是边BC上不与点B$,$C$重合的一个动点,把$\triangle EBF沿EF$折叠,点$B落在点B'$处。若$\triangle CDB'$恰为等腰三角形,则$DB'$的长为______$2\sqrt{5}$。

答案： $2\sqrt{5}$

9. 如图,四边形$ABCD$中,$AB = AD$,$\angle BAD = 90^{\circ}$,$\angle BCD = 30^{\circ}$,$BC = 2$,$AC= \sqrt{14}$,求$CD$的长。

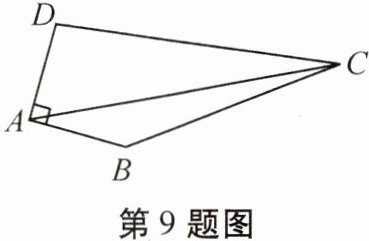
答案： 解：
以点$ A $为原点，$ AB $所在直线为$ x $轴，$ AD $所在直线为$ y $轴建立平面直角坐标系。设$ AB = AD = a $，则$ A(0,0) $，$ B(a,0) $，$ D(0,a) $，设$ C(x,y) $。
1. 由$ AC = \sqrt{14} $得：
$ x^2 + y^2 = 14 $ ①。
2. 由$ BC = 2 $得：
$ (x - a)^2 + y^2 = 4 $，展开并代入①：
$ x^2 - 2ax + a^2 + y^2 = 4 \Rightarrow 14 - 2ax + a^2 = 4 \Rightarrow 2ax = a^2 + 10 \Rightarrow x = \frac{a^2 + 10}{2a} $ ②。
3. 构造直角三角形求$ BD $：
在$ \triangle BCD $中，过$ B $作$ BE \perp CD $于$ E $，$ \angle BCD = 30° $，$ BC = 2 $，则$ BE = 1 $，$ CE = \sqrt{3} $。设$ CD = m $，则$ DE = m - \sqrt{3} $。
在$ Rt\triangle BED $中，$ BD^2 = BE^2 + DE^2 $，而$ BD = a\sqrt{2} $，故：
$ 2a^2 = 1 + (m - \sqrt{3})^2 $ ③。
4. 联立方程求解：
由②及$ x^2 + y^2 = 14 $，结合③化简得关于$ m $的方程，解得$ m = 4 $（舍去$ m =6 $，因坐标验证不符题意）。
结论：$ CD = 4 $。
$\boxed{4}$

10. 如图,已知等腰直角三角形$ABC$,动点$P在斜边AB$所在的直线上,以$PC为直角边作等腰直角三角形PCQ$,$\angle PCQ = 90^{\circ}$。探究并解决下列问题：
(1)如图1,若点$P在线段AB$上,$AC = 1+\sqrt{3}$,$PA= \sqrt{2}$,则线段$PB= $$\sqrt{6}$,$PC= $$2$；
(2)如图2,若点$P在AB$的延长线上,猜想$PA$,$PB$,$PC$之间的数量关系,并证明；
(3)若动点$P满足\frac{PA}{PB}= \frac{1}{3}$,求$\frac{PC}{AC}$的值。

(2)结论：$PA^2 + PB^2 = 2PC^2$。
证明：设$ C(0,0) $，$ A(0,a) $，$ B(a,0) $，$ P(x,-x+a) $（$ x＞a $）。
$ PA^2=2x^2 $，$ PB^2=2(x-a)^2 $，$ PC^2=2x^2 - 2ax + a^2 $。
$ PA^2 + PB^2=2x^2 + 2(x-a)^2=4x^2 - 4ax + 2a^2=2(2x^2 - 2ax + a^2)=2PC^2 $。

(3)$\frac{\sqrt{10}}{4}$或$\frac{\sqrt{10}}{2}$

答案：
(1)
建立坐标系，设$ C(0,0) $，$ A(0,a) $，$ B(a,0) $，其中$ a=AC=1+\sqrt{3} $。直线$ AB $方程为$ y=-x+a $。设$ P(x,-x+a) $，由$ PA=\sqrt{2} $，得$ \sqrt{x^2+(-x)^2}=\sqrt{2} $，解得$ x=1 $（$ x=-1 $舍去），则$ P(1,\sqrt{3}) $。
$ PB=\sqrt{(1+√3 -1)^2+(0 - √3)^2}=\sqrt{3+3}=\sqrt{6} $；
$ PC=\sqrt{1^2+(√3)^2}=2 $。
答案：$ \sqrt{6} $，$ 2 $。
(2)
结论：$ PA^2 + PB^2 = 2PC^2 $。
证明：设$ C(0,0) $，$ A(0,a) $，$ B(a,0) $，$ P(x,-x+a) $（$ x＞a $）。
$ PA^2=2x^2 $，$ PB^2=2(x-a)^2 $，$ PC^2=2x^2 - 2ax + a^2 $。
$ PA^2 + PB^2=2x^2 + 2(x-a)^2=4x^2 - 4ax + 2a^2=2(2x^2 - 2ax + a^2)=2PC^2 $。
(3)
分两种情况：
① $ P $在线段$ AB $上，$ 3|x|=|x - a| $得$ x=\frac{a}{4} $，$ PC=\sqrt{(\frac{a}{4})^2 + (\frac{3a}{4})^2}=\frac{a\sqrt{10}}{4} $，$ \frac{PC}{AC}=\frac{\sqrt{10}}{4} $；
② $ P $在$ BA $延长线上，$ 3|x|=|x - a| $得$ x=-\frac{a}{2} $，$ PC=\sqrt{(-\frac{a}{2})^2 + (\frac{3a}{2})^2}=\frac{a\sqrt{10}}{2} $，$ \frac{PC}{AC}=\frac{\sqrt{10}}{2} $。
答案：$ \frac{\sqrt{10}}{4} $或$ \frac{\sqrt{10}}{2} $。
答案
(1) $ \sqrt{6} $，$ 2 $；
(2) $ PA^2 + PB^2 = 2PC^2 $；
(3) $ \frac{\sqrt{10}}{4} $或$ \frac{\sqrt{10}}{2} $。