《2025年学典四川八年级数学上册北师大版》

10. 草莓销售季节某种植基地开发了草莓采摘无人销售方式,为方便小朋友体验,销售人员列出销售的草莓质量$x$(单位：$kg$)与销售总价$y$(单位：元)之间的关系如表：
|销售质量$x/kg$|1|2|3|4|…|
|销售总价$y/元$|8.5|16.5|24.5|32.5|…|

(1)写出$y与x$之间的函数关系式；
(2)丽丽一家共摘了$6.5kg$草莓,应付多少钱？

答案： （1）设函数关系式为$y = kx + b$，从表格中选取两组数据$(1,8.5)$，$(2,16.5)$代入函数关系式，可得$\begin{cases}k + b = 8.5,\\2k + b = 16.5.\end{cases}$解得$\begin{cases}k = 8,\\b = 0.5.\end{cases}$所以$y$与$x$之间的函数关系式为$y = 8x + 0.5$。
（2）当$x = 6.5$时，$y=8×6.5 + 0.5 = 52.5$（元）。
综上，应付$52.5$元。

11. 根据如图所示的运算程序,解答问题：
(1)若输入$x = - 7$,请计算输出的结果$y$的值；
(2)若输入一个正数$x$,输出$y的值为12$,则输入的$x$值可能是多少？

答案： （1）输入$x = -7$，因为$-7＜0$，所以$y = \sqrt{5 - (-7)} = \sqrt{12} = 2\sqrt{3}$；
（2）当$0\leq x＜2$时，令$3x + 7 = 12$，解得$x =\frac{5}{3}$，满足$0\leq x＜2$；
当$x\geq2$时，令$x^3 - 15 = 12$，即$x^3=27$，解得$x = 3$，满足$x\geq2$。
综上，输入的$x$值可能是$\frac{5}{3}$或$3$。
故答案为：（1）$2\sqrt{3}$；（2）$\frac{5}{3}$或$3$。

12. 中国古代有很多极为精巧的发明,榫卯结构就是其一,它是在两个木构件上所采用的一种凹凸结合的连接方式. 如图,已知一个木构件的长度为$6$,其凸出部分的长为$1$,若当$x$个相同的木构件紧密拼成一列时,其总长度为$y$,则$y与x$之间的关系式为y=5x+1.

答案： y=5x+1

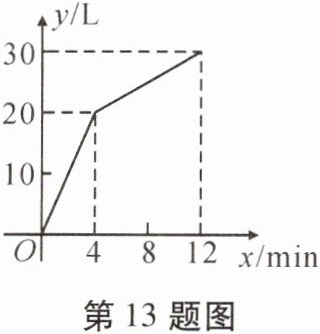
13. 一个有进水管和出水管的容器,从某时刻开始$4min$内只进水不出水,在随后的$8min$内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量$y$(单位：$L$)与时间$x$(单位：$min$)之间的函数关系如图所示,则每分钟的出水量为3.75.

答案： 3.75

14. 出租车收费按路程计算,$3$千米以内(含$3$千米)收费$8$元,超过$3$千米时,每$1千米加收1.80$元.
(1)写出车费$y$(单位：元)与路程$x$(单位：千米)之间的函数关系式；
(2)某人在离家$8$千米处,身上仅有$18$元,问他的钱够乘出租车回家吗？

答案：
(1)
当$0\lt x\leqslant3$时，$y = 8$；
当$x\gt3$时，$y=8 + 1.8(x - 3)=1.8x+2.6$。
函数关系式为$y=\begin{cases}8(0\lt x\leqslant3)\\1.8x + 2.6(x\gt3)\end{cases}$。
(2)
当$x = 8$时，$y=1.8×8+2.6=14.4 + 2.6=17$（元）。
因为$17\lt18$，所以他的钱够乘出租车回家。