《2025年新课程能力培养七年级数学上册人教版》

16. (每小题 5 分,共 10 分)
已知∠α= 76°42',∠β= 41°41'.
(1)求∠β 的余角.
(2)求∠α 与∠β 的 2 倍的和.

答案： 解：（1）
∵∠β=41°41'，
∴∠β的余角=90°-∠β=90°-41°41'=48°19'.
（2）
∵∠α=76°42'，∠β=41°41'，
∴∠α+2∠β=76°42'+2×41°41'=76°42'+82°82'=158°124'=160°4'.

17. (本小题 8 分)
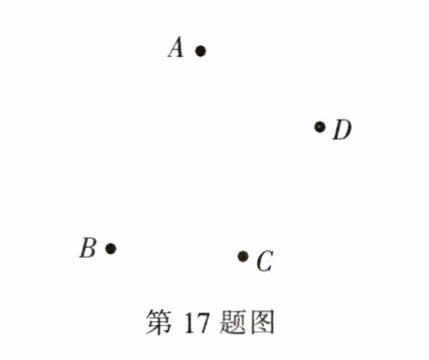
如图,在同一平面内有四个点 A,B,C,D,请按要求完成下列问题.(注此题作图不要求写出画法和结论)
(1)作射线 AC.
(2)作直线 BD 与射线 AC 相交于点 O.
(3)分别连接 AB,AD.
(4)我们容易判断出线段 AB+AD 与 BD 的数量关系是______,理由是______.

答案：
解：（1）（2）（3）如图所示.

（4）AB+AD＞BD，两点之间，线段最短.

18. (本小题 8 分)
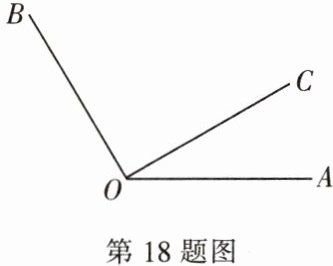
如图,已知∠AOB= 120°,OC 是∠AOB 内的一条射线,且∠AOC:∠BOC= 1:2.
(1)求∠AOC 的度数.
(2)过点 O 作射线 OD,若∠AOD= $\frac{1}{2}$∠AOB,求∠COD 的度数.

答案： 解：（1）
∵∠AOC:∠BOC=1:2，∠AOB=120°，
∴∠AOC=$\frac{1}{3}$∠AOB=$\frac{1}{3}$×120°=40°.
（2）
∵∠AOD=$\frac{1}{2}$∠AOB，
∴∠AOD=60°.当OD在∠AOB内时，∠COD=∠AOD-∠AOC=20°；当OD在∠AOB外时，∠COD=∠AOC+∠AOD=100°.故∠COD的度数为20°或100°.