第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
3. 把体积为1立方分米的正方体纸盒放在桌面上,纸盒所占桌面的面积(
A.等于
B.小于
C.大于
A
)1平方分米。A.等于
B.小于
C.大于
答案:
解析:本题考查正方体一个面的面积计算。
正方体有6个面,且每个面都是正方形,面积都相等。
已知正方体的体积为1立方分米,因为正方体的体积=棱长×棱长×棱长,且1×1×1=1(立方分米),所以正方体的棱长为1分米。
正方体底面为正方形,正方形面积=边长×边长,所以纸盒所占桌面的面积(即正方体一个面的面积)为1×1=1(平方分米)。
答案:A。
正方体有6个面,且每个面都是正方形,面积都相等。
已知正方体的体积为1立方分米,因为正方体的体积=棱长×棱长×棱长,且1×1×1=1(立方分米),所以正方体的棱长为1分米。
正方体底面为正方形,正方形面积=边长×边长,所以纸盒所占桌面的面积(即正方体一个面的面积)为1×1=1(平方分米)。
答案:A。
4. 体育馆新建了一个长方体游泳池,长90米,宽25米,深3米。现在要把游泳池的四周和底面都贴上瓷砖,计算贴瓷砖的面积一共是多少平方米,列式正确的是(
A.$90×25×2+25×3×2+90×3$
B.$90×3×2+90×25×2+25×3$
C.$(90×25+90×3+25×3)×2-90×25$
C
)。A.$90×25×2+25×3×2+90×3$
B.$90×3×2+90×25×2+25×3$
C.$(90×25+90×3+25×3)×2-90×25$
答案:
解析:
本题考查长方体的表面积计算。
题目中描述的是一个长方体游泳池,其长是90米,宽是25米,深是3米,要把这个游泳池的四周和底面都贴上瓷砖,所以我们需要计算长方体的五个面(底面加四个侧面)的面积。
长方体的底面积为长$×$宽,两个侧面的面积为$2×$(长$×$深),另外两个侧面的面积为$2×$(宽$×$深)。
所以,贴瓷砖的总面积为底面积加上四个侧面的面积,即$90× 25 + 2×(90× 3) + 2×(25× 3)$。
这个表达式可以简化为$(90× 25 + 90× 3 + 25× 3)× 2 - 90× 25$,因为底面被重复计算了一次,所以需要减去一次$90× 25$。
或者也可以直接计算五个面的面积和:$90× 25 + 90× 3× 2 + 25× 3× 2$。
对比选项,我们发现选项C的表达式与我们计算的结果一致,只是形式稍有不同,它是先算出了所有面的面积和的两倍,然后减去了多算的一次底面积。而选项A和B的表达式与我们计算的结果不符。
答案:C。
本题考查长方体的表面积计算。
题目中描述的是一个长方体游泳池,其长是90米,宽是25米,深是3米,要把这个游泳池的四周和底面都贴上瓷砖,所以我们需要计算长方体的五个面(底面加四个侧面)的面积。
长方体的底面积为长$×$宽,两个侧面的面积为$2×$(长$×$深),另外两个侧面的面积为$2×$(宽$×$深)。
所以,贴瓷砖的总面积为底面积加上四个侧面的面积,即$90× 25 + 2×(90× 3) + 2×(25× 3)$。
这个表达式可以简化为$(90× 25 + 90× 3 + 25× 3)× 2 - 90× 25$,因为底面被重复计算了一次,所以需要减去一次$90× 25$。
或者也可以直接计算五个面的面积和:$90× 25 + 90× 3× 2 + 25× 3× 2$。
对比选项,我们发现选项C的表达式与我们计算的结果一致,只是形式稍有不同,它是先算出了所有面的面积和的两倍,然后减去了多算的一次底面积。而选项A和B的表达式与我们计算的结果不符。
答案:C。
5. 用几个体积为1立方厘米的正方体木块摆一个物体,如图所示是从不同方向看到的图形。这个物体的体积至少是(

A.7
B.8
C.9
B
)立方厘米。 
A.7
B.8
C.9
答案:
从上面看,物体底层有5个正方体。从前面看,物体有3层,从左面看,物体有3层。综合前面和左面视图,第二层至少有2个正方体,第三层至少有1个正方体。5+2+1=8。答案:B.8
6. 一个长方体的底面是面积为9平方分米的正方形,它的侧面展开图正好是一个正方形。这个长方体的表面积是(
A.90
B.144
C.162
162
)平方分米。A.90
B.144
C.162
答案:
解析:本题考查的是长方体的表面积计算。
首先,长方体的底面是一个面积为9平方分米的正方形。
根据正方形面积=边长×边长,可得:
边长×边长=9
由于3×3=9,所以正方形的边长为3分米。
又因为长方体的侧面展开图正好是一个正方形,说明长方体的高等于底面周长。
根据正方形周长=边长×4,可得:
底面周长为:3×4=12(分米)。
所以,长方体的高也是12分米。
接下来,计算长方体的表面积。
长方体的表面积由底面和四个侧面组成。
底面的面积已经给出,为9平方分米。
因为长方体有两个底面,所以两个底面的总面积是:
9×2=18(平方分米)
每个侧面的面积是底面边长乘以高,即:
3×12=36(平方分米)
由于长方体有四个侧面,所以四个侧面的总面积是:
36×4=144(平方分米)
最后,长方体的表面积为两个底面的总面积加上四个侧面的总面积:
18+144=162(平方分米)
所以,这个长方体的表面积是162平方分米,
答案为C。
首先,长方体的底面是一个面积为9平方分米的正方形。
根据正方形面积=边长×边长,可得:
边长×边长=9
由于3×3=9,所以正方形的边长为3分米。
又因为长方体的侧面展开图正好是一个正方形,说明长方体的高等于底面周长。
根据正方形周长=边长×4,可得:
底面周长为:3×4=12(分米)。
所以,长方体的高也是12分米。
接下来,计算长方体的表面积。
长方体的表面积由底面和四个侧面组成。
底面的面积已经给出,为9平方分米。
因为长方体有两个底面,所以两个底面的总面积是:
9×2=18(平方分米)
每个侧面的面积是底面边长乘以高,即:
3×12=36(平方分米)
由于长方体有四个侧面,所以四个侧面的总面积是:
36×4=144(平方分米)
最后,长方体的表面积为两个底面的总面积加上四个侧面的总面积:
18+144=162(平方分米)
所以,这个长方体的表面积是162平方分米,
答案为C。
1. 如图所示是用棱长为1厘米的正方体摆成的物体。
(1)从前面、上面和右面看到的分别是什么形状?试着画一画。
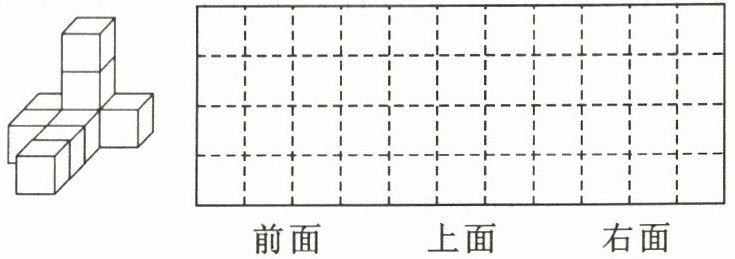
(2)这个物体的表面积是( )平方厘米。
(3)至少添加( )个同样的小正方体可以补成一个长方体,这个长方体的表面积是( )平方厘米。
(1)从前面、上面和右面看到的分别是什么形状?试着画一画。

(2)这个物体的表面积是( )平方厘米。
(3)至少添加( )个同样的小正方体可以补成一个长方体,这个长方体的表面积是( )平方厘米。
答案:
(1)
(2) 28
(3) 11;54
(1)
(2) 28
(3) 11;54
查看更多完整答案,请扫码查看


