《2025年多维互动提优课堂六年级数学上册苏教版提升版》

9. 正方形的周长与它的边长的比是4:1；正方体的表面积与它的一个面的面积的比是6:1。

答案： 解析：
第一个空，考查正方形的周长与边长的关系。正方形的周长是其边长的四倍。因此，正方形的周长与它的边长的比是4与1的比，即4:1。
第二个空，考查正方体的表面积与一个面的面积的关系。正方体有6个面，每个面的面积都是边长的平方。因此，正方体的总表面积是一个面的面积的6倍。所以，正方体的表面积与一个面的面积的比是6与1的比，即6:1。
答案：
4:1；6:1。

10. 把一根长50分米的长方体木料沿着横截面截成三段后,表面积增加了30平方分米。横截面是(7.5)平方分米,原来这根木料的体积是(375)立方分米。

答案： 解析：本题考查了长方体的体积公式。
一个长方体被截成三段，需要截两次，每截一次增加两个截面，所以共增加了$2×2=4(个)÷ $截面，已知表面积增加了30平方分米，所以横截面的面积是$30÷4=7.5(平方分米)$。
长方体体积=横截面面积$×$长
$V= 7.5×50=375(立方分米)$。
答案：7.5；375。

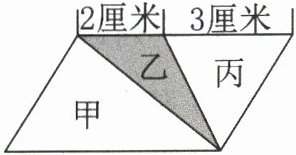
11. 如图,平行四边形的面积是20平方厘米,甲、乙两个三角形的面积比是(2:3),三角形乙的面积是(6)平方厘米。

答案： 解析：本题主要考查三角形与四边形面积的关系及面积的计算。
甲和乙三角形的高与平行四边形的高相等，丙三角形的高也与平行四边形的高相等。
设平行四边形的高为h，
平行四边形的面积公式为底乘以高，
所以$2 + 3) × h = 20$，
$5h = 20$，
$h = 4$（厘米）。
三角形的面积公式为底乘以高的一半，
三角形甲的面积：
$\frac{1}{2} × 2 × h = \frac{1}{2} × 2 × 4 = 4 $（平方厘米），
三角形乙的面积：
$\frac{1}{2} × 3 × h = \frac{1}{2} × 3 × 4 = 6 $（平方厘米），
三角形丙的面积和平行四边形的面积减去三角形甲和乙的面积：
$20 - 4 - 6 = 10 - 6 = 4$（平方厘米），
甲、乙两个三角形的面积比：
$4 : 6 = 2 : 3$。
答案为：$2 : 3$；$6$。

12. 一个等腰三角形的两个内角的度数比是2:5。如果它是锐角三角形,那么顶角的度数是(30°)；如果它是钝角三角形,那么顶角的度数是(100°)。

答案： 情况一（锐角三角形）：
内角比为2:5:5，总份数2+5+5=12，每份180°÷12=15°，顶角占2份，15°×2=30°。
情况二（钝角三角形）：
内角比为2:2:5，总份数2+2+5=9，每份180°÷9=20°，顶角占5份，20°×5=100°。
30°；100°

1. 计算$1 ÷ \frac{4}{5}$时,两名同学用不同的方法表达了自己的想法,这两名同学计算的依据是(A)。
① 宁宁：$1 ÷ \frac{4}{5}= (1 × 5) ÷ (\frac{4}{5} × 5)= 1.25$
② 君君：$1 ÷ \frac{4}{5}= 1 ÷ (4 ÷ 5)= 1 ÷ 0.8= 1.25$
A.宁宁：商不变的规律；君君：分数与除法的关系
B.宁宁：乘法和除法的关系；君君：除法的意义
C.宁宁：商不变的规律；君君：除法的意义

答案： 解析：
本题考查的是商不变的规律以及分数与除法的关系。
首先分析宁宁的方法：
宁宁将原式 $1÷\frac{4}{5}$ 的被除数和除数同时乘以5，得到 $(1×5)÷(\frac{4}{5}×5)=5÷4=1.25$，
这里，宁宁利用了“商不变的规律”，即被除数和除数同时乘以或除以同一个不为0的数，商不变。
接着分析君君的方法：
君君首先将 $\frac{4}{5}$ 转化为小数 $0.8$，然后计算 $1÷0.8=1.25$，
这里，君君实际上利用了“分数与除法的关系”，即分数可以转化为除法运算，进而转化为小数进行计算。
综合以上分析，宁宁依据的是商不变的规律，君君依据的是分数与除法的关系。
答案：A。

2. 对下面消毒液使用说明中“1：52”理解错误的是(C)。
| 消毒液使用说明 |
| 衣服消毒 机洗、漂洗:在洗涤过程中按1:52的比加入原液和水。 |
A.1份原液配52份水
B.如果放20毫升原液,就要放1040毫升水
C.原液占稀释后液体总量的$\frac{1}{52}$

答案： 解析：
题目考查的是对比例的理解。
A选项表示的是1份原液配52份水，这是“1:52”比例的直接解读，所以A选项是正确的。
B选项表示的是如果放20毫升原液，就要放1040毫升水。根据“1:52”的比例，20毫升原液应该配20×52=1040毫升水，所以B选项也是正确的。
C选项表示的是原液占稀释后液体总量的$\frac{1}{52}$。然而，根据“1:52”的比例，原液应该占稀释后液体总量的$\frac{1}{1+52}=\frac{1}{53}$，而不是$\frac{1}{52}$。所以C选项是错误的。
答案：C