《2025年同步测控优化设计七年级数学上册人教精编版》

1. 解下列方程时,合并同类项不正确的是(C)
A.$5x - 4x = 1$,合并同类项,得$x = 1$
B.$3x - 5x = - 2$,合并同类项,得$- 2x = - 2$
C.$2x - 3x - 4x = 1$,合并同类项,得$x = 1$
D.$\frac{1}{2}x + \frac{1}{3}x = 2$,合并同类项,得$\frac{5}{6}x = 2$

答案： C

2. 一元一次方程$x + 3x = 8$的解是(D)
A.$x = - 1$
B.$x = 0$
C.$x = 1$
D.$x = 2$

答案： D

3. 根据题意,列出关于$x$的方程(不必解方程)：
某农场有试验田$1080m^{2}$,全部用来种植$A$,$B$,$C$三种农作物。已知三种农作物的种植面积比是$2:3:4$,求三种农作物的种植面积分别是多少。
解：设$A种农作物的种植面积为2x m^{2}$,则$B$,$C两种农作物的种植面积分别为3x m^{2}$,$4x m^{2}$,根据试验田总面积为$1080m^{2}$,列出方程$2x+3x+4x=1080$。

答案： $2x+3x+4x=1080$

4. 解下列方程：
(1)$- 3x + 0.5x = 2$；
(2)$7x - 2x = 8 + 2$；
(3)$\frac{1}{3}x - x = 5 - 1$；
(4)$- \frac{3}{2}x - 3x = 2.5 - 1$。

答案： 解
(1)合并同类项,得$-2.5x=2$.
系数化为1,得$x=-0.8$.
(2)合并同类项,得$5x=10$.
系数化为1,得$x=2$.
(3)合并同类项,得$-\frac{2}{3}x=4$.
系数化为1,得$x=-6$.
(4)合并同类项,得$-\frac{9}{2}x=\frac{3}{2}$.
系数化为1,得$x=-\frac{1}{3}$.

5. 某学校要种$506$棵松树,把任务分给七、八、九三个年级。已知九年级分到的松树棵数的$\frac{1}{5}与八年级分到的松树棵数的\frac{1}{4}$相等,同时又都等于七年级分到的松树棵数的$\frac{1}{2}$,求七年级分到多少棵松树？

答案： 解 设七年级分到x棵松树,
则九年级分到的松树棵数为$\frac{1}{2}x÷\frac{1}{5}=\frac{5}{2}x$,八年级分到的松树棵数为$\frac{1}{2}x÷\frac{1}{4}=2x$.
根据三个年级栽种松树的数量之和等于总棵数,列得方程$x+\frac{5}{2}x+2x=506$,解得$x=92$.
答:七年级分到92棵松树.

6. 老师在黑板上写出下列算式：
$\boxed{7 × □ - 5 × \triangle =?}$

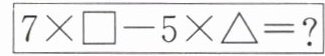
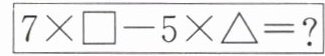
(1) 请你在“$□$”和“$\triangle$”中分别填入一个数,并计算其结果。
(2) 嘉嘉在“$□$”中填入$- 6$,得到的结果是$- 38$,则嘉嘉在“$\triangle$”处填入的数是多少？
(3) 淇淇说,在“$□$”和“$\triangle$”中可以填入一个相同的负数,使计算结果为$- 2$,则她填入的数是-1。

答案： -1