4. (2025·重庆期中)在△ABC中,AB= AC,AC上的中线BD把三角形的周长分成24和30两部分,则底边BC的长为______.
答案:
22或14 [解析]由题意,得AD = CD,
∴AB = AC = 2AD.
当AB + AD = 24时,即2AD + AD = 24,
∴AD = 8.
∵BC + CD = 30,
∴BC = 30 - CD = 30 - 8 = 22;
当AB + AD = 30时,即2AD + AD = 30,
∴AD = 10.
∵BC + CD = 24,
∴BC = 24 - CD = 24 - 10 = 14.
综上所述,底边BC的长为22或14.
∴AB = AC = 2AD.
当AB + AD = 24时,即2AD + AD = 24,
∴AD = 8.
∵BC + CD = 30,
∴BC = 30 - CD = 30 - 8 = 22;
当AB + AD = 30时,即2AD + AD = 30,
∴AD = 10.
∵BC + CD = 24,
∴BC = 24 - CD = 24 - 10 = 14.
综上所述,底边BC的长为22或14.
例5 已知等腰三角形一腰上的高与另一腰的夹角是40°,求这个等腰三角形的底角的度数.
解答 应分两种情况求解.
①当等腰三角形是锐角三角形时,如图(1),可设AB= AC,则∠B= ∠ACB.
因为∠ACD= 40°,则∠A= 50°,
所以∠B= ∠ACB= $\frac{1}{2}$×(180°-∠A)= $\frac{1}{2}$×(180°-50°)= 65°.
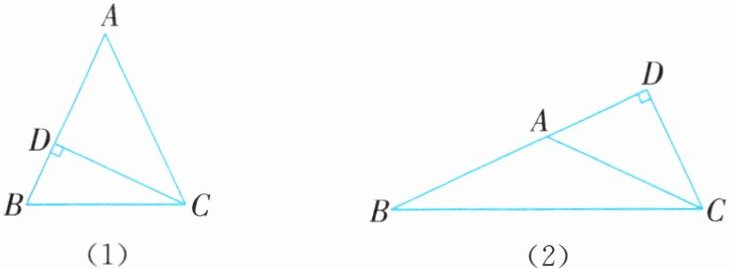
②当等腰三角形是钝角三角形时,如图(2),可设AB= AC,则∠B= ∠ACB.
因为∠ACD= 40°,所以∠DAC= 50°,
所以∠BAC= 130°,
所以∠B= ∠ACB= $\frac{1}{2}$×(180°-∠BAC)= $\frac{1}{2}$×(180°-130°)= 25°.
故这个等腰三角形的底角的度数是65°或25°.
辨析归纳
在解有关等腰三角形的问题时,应认真审题.若等腰三角形的顶角是锐角,则腰上的高在三角形的内部;若等腰三角形的顶角是钝角,则腰上的高在三角形外部,题中没有明确三角形的情况,要分情况讨论.
解答 应分两种情况求解.
①当等腰三角形是锐角三角形时,如图(1),可设AB= AC,则∠B= ∠ACB.
因为∠ACD= 40°,则∠A= 50°,
所以∠B= ∠ACB= $\frac{1}{2}$×(180°-∠A)= $\frac{1}{2}$×(180°-50°)= 65°.

②当等腰三角形是钝角三角形时,如图(2),可设AB= AC,则∠B= ∠ACB.
因为∠ACD= 40°,所以∠DAC= 50°,
所以∠BAC= 130°,
所以∠B= ∠ACB= $\frac{1}{2}$×(180°-∠BAC)= $\frac{1}{2}$×(180°-130°)= 25°.
故这个等腰三角形的底角的度数是65°或25°.
辨析归纳
在解有关等腰三角形的问题时,应认真审题.若等腰三角形的顶角是锐角,则腰上的高在三角形的内部;若等腰三角形的顶角是钝角,则腰上的高在三角形外部,题中没有明确三角形的情况,要分情况讨论.
答案:
65°或25° [解析]应分两种情况求解.
①当等腰三角形是锐角三角形时,如图
(1),可设AB= AC,则∠B= ∠ACB.
因为∠ACD= 40°,则∠A= 50°,
所以∠B= ∠ACB= $\frac{1}{2}$×(180°-∠A)= $\frac{1}{2}$×(180°-50°)= 65°.

②当等腰三角形是钝角三角形时,如图
(2),可设AB= AC,则∠B= ∠ACB.
因为∠ACD= 40°,所以∠DAC= 50°,
所以∠BAC= 130°,
所以∠B= ∠ACB= $\frac{1}{2}$×(180°-∠BAC)= $\frac{1}{2}$×(180°-130°)= 25°.
故这个等腰三角形的底角的度数是65°或25°.
65°或25° [解析]应分两种情况求解.
①当等腰三角形是锐角三角形时,如图
(1),可设AB= AC,则∠B= ∠ACB.
因为∠ACD= 40°,则∠A= 50°,
所以∠B= ∠ACB= $\frac{1}{2}$×(180°-∠A)= $\frac{1}{2}$×(180°-50°)= 65°.

②当等腰三角形是钝角三角形时,如图
(2),可设AB= AC,则∠B= ∠ACB.
因为∠ACD= 40°,所以∠DAC= 50°,
所以∠BAC= 130°,
所以∠B= ∠ACB= $\frac{1}{2}$×(180°-∠BAC)= $\frac{1}{2}$×(180°-130°)= 25°.
故这个等腰三角形的底角的度数是65°或25°.
5. (2025·宿迁宿城区期中)若等腰三角形的两条高所在直线形成的角中有一个为45°,则其顶角的度数为______.
答案:
45°或90°或135° [解析]分情况讨论:
①如图
(1),AB = AC,∠BFE = 45°,

∵CE⊥AB,BD⊥AC,
∴∠BEC = ∠ADB = ∠BDC = 90°,
∴∠ABD = ∠A = 45°,即顶角为45°.
②如图
(2),AB = AC,∠BAD = 45°,

∵AD⊥BC,
∴∠ADB = ∠ADC = 90°,
∴∠BAD = ∠B = 45°,
∴∠B = ∠C = 45°,
∴∠BAC = 90°,即顶角为90°.
③如图
(3),AB = AC,∠BPC = 45°,

同①理可得∠PBN = ∠BAM = 45°,
∴∠BAC = 135°,即顶角为135°.
综上所述,顶角度数为45°或90°或135°.
45°或90°或135° [解析]分情况讨论:
①如图
(1),AB = AC,∠BFE = 45°,

∵CE⊥AB,BD⊥AC,
∴∠BEC = ∠ADB = ∠BDC = 90°,
∴∠ABD = ∠A = 45°,即顶角为45°.
②如图
(2),AB = AC,∠BAD = 45°,

∵AD⊥BC,
∴∠ADB = ∠ADC = 90°,
∴∠BAD = ∠B = 45°,
∴∠B = ∠C = 45°,
∴∠BAC = 90°,即顶角为90°.
③如图
(3),AB = AC,∠BPC = 45°,

同①理可得∠PBN = ∠BAM = 45°,
∴∠BAC = 135°,即顶角为135°.
综上所述,顶角度数为45°或90°或135°.
例1 (2025·湖南长沙宁乡期末)如图,书架两侧摆放了若干本相同的书籍,左右两摞书中竖直放入一个等腰直角三角板,其直角顶点C在书架底部DE上,当顶点A落在右侧书籍的上方边沿时,顶点B恰好落在左侧书籍的上方边沿.已知每本书长20cm,厚度为2cm,则两摞书之间的距离DE为( ).

A. 24cm
B. 23cm
C. 22cm
D. 21cm
解析 由题意可得AC= BC,∠ACB= 90°,BD⊥DE,AE⊥DE,
∴∠BDC= ∠CEA= 90°,
∴∠BCD+∠ACE= 90°,∠BCD+∠DBC= 90°,∴∠ACE= ∠DBC.
在△BDC和△CEA中,$\begin{cases} ∠BDC= ∠CEA, \\ ∠DBC= ∠ECA, \\ BC= CA, \end{cases} $
∴△BDC≌△CEA(AAS).
由题意可得BD= EC= 4cm,DC= AE= 20cm.
∴DE= DC+CE= 24cm.
答案 A
点拨
本题考查了全等三角形的应用.做题时要注意找已知条件,根据已知得出全等三角形是解题关键.

A. 24cm
B. 23cm
C. 22cm
D. 21cm
解析 由题意可得AC= BC,∠ACB= 90°,BD⊥DE,AE⊥DE,
∴∠BDC= ∠CEA= 90°,
∴∠BCD+∠ACE= 90°,∠BCD+∠DBC= 90°,∴∠ACE= ∠DBC.
在△BDC和△CEA中,$\begin{cases} ∠BDC= ∠CEA, \\ ∠DBC= ∠ECA, \\ BC= CA, \end{cases} $
∴△BDC≌△CEA(AAS).
由题意可得BD= EC= 4cm,DC= AE= 20cm.
∴DE= DC+CE= 24cm.
答案 A
点拨
本题考查了全等三角形的应用.做题时要注意找已知条件,根据已知得出全等三角形是解题关键.
答案:
A [解析]由题意可得AC= BC,∠ACB= 90°,BD⊥DE,AE⊥DE,
∴∠BDC= ∠CEA= 90°,
∴∠BCD+∠ACE= 90°,∠BCD+∠DBC= 90°,
∴∠ACE= ∠DBC.
在△BDC和△CEA中,$\begin{cases} ∠BDC= ∠CEA, \\ ∠DBC= ∠ECA, \\ BC= CA, \end{cases} $
∴△BDC≌△CEA(AAS).
由题意可得BD= EC= 4cm,DC= AE= 20cm.
∴DE= DC+CE= 24cm.
答案 A
∴∠BDC= ∠CEA= 90°,
∴∠BCD+∠ACE= 90°,∠BCD+∠DBC= 90°,
∴∠ACE= ∠DBC.
在△BDC和△CEA中,$\begin{cases} ∠BDC= ∠CEA, \\ ∠DBC= ∠ECA, \\ BC= CA, \end{cases} $
∴△BDC≌△CEA(AAS).
由题意可得BD= EC= 4cm,DC= AE= 20cm.
∴DE= DC+CE= 24cm.
答案 A
查看更多完整答案,请扫码查看


