《2025年实验班提优训练八年级数学上册苏科版》

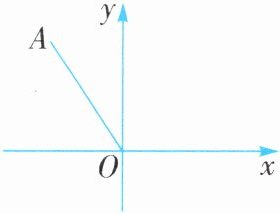
例4 (2024·湖北中考)如图,点A的坐标是(-4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( ).


A.(4,6)
B.(6,4)
C.(-6,-4)
D.(-4,-6)
名师启发 根据题意画出旋转后的图形,再结合全等三角形的判定与性质即可解决问题.
🔔关键提醒
图形或点旋转之后,要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标是解题的关键.

答案： B　[解析]如图所示，分别过点A和点B作x轴的垂线，垂足分别为M和N,由旋转可知,OA=OB,∠AOB=90°,
∴∠AOM+∠BON=∠A+∠AOM=90°,
∴∠A=∠BON.在△AOM和△OBN中，{∠AMO=∠ONB,∠A=∠BON,OA=BO,
∴△AOM≌△OBN(AAS),
∴BN=MO,ON=AM.
∵点A的坐标为(−4,6),
∴BN=MO=4,ON=AM=6,
∴点B的坐标为(6,4).故选B.

例5 (2024·凉山州中考)点P(a,-3)关于原点对称的点是P'(2,b),则a+b的值是( ).

A.1
B.-1
C.-5
D.5
名师启发 利用关于原点对称的点的坐标特点,即可解答.
🔔关键提醒
解题的关键是理解题意,熟练掌握关于原点对称的点的坐标特征.

答案： A　[解析]
∵点P(a,−3)关于原点对称的点是P'(2,b),
∴a=−2,b=3,
∴a+b=1.故选A.

例6 如图,在平面直角坐标系中,△AOB是直角三角形,∠OAB= 90°,OA= 8,AB= 6,则点A关于y轴的对称点的坐标为______.

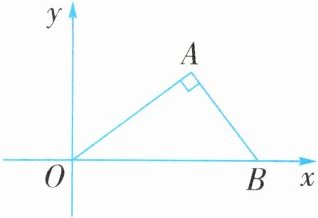
名师启发 首先直接利用勾股定理得出BO的长,再利用直角三角形面积得出斜边上的高的长,进而得出A点坐标,即可得出点A关于y轴的对称点的坐标.
🔔关键提醒
本题主要考查了勾股定理以及直角三角形面积求法,正确得出斜边上的高是解题关键.

答案： (−$\frac{32}{5}$,$\frac{24}{5}$)　[解析]如图,过点A作AC⊥OB于点C.
∵△AOB是直角三角形，∠OAB=90°,OA=8,AB=6,
∴BO²=8²+6²=100,
∴BO=10,
∴AC·BO=AO·AB,
∴AC=$\frac{AO·AB}{BO}$=$\frac{6×8}{10}$=$\frac{24}{5}$,
∴CO²=OA²−AC²=8²−($\frac{24}{5}$)²=($\frac{32}{5}$)²,
∴CO=$\frac{32}{5}$,
∴点A坐标为($\frac{32}{5}$,$\frac{24}{5}$),
∴点A关于y轴的对称点的坐标为(−$\frac{32}{5}$,$\frac{24}{5}$).

例7 (2025·苏州期末)如图,在平面直角坐标系中,点A(0,4)、点C(4,1),连接AC,点D是x轴上一点,若△ACD是以AC为底边的等腰三角形,则D点的坐标为______.

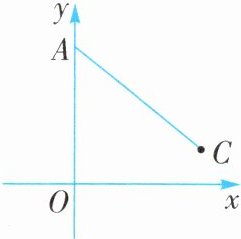
名师启发 设D(m,0),根据两点间距离公式,结合等腰三角形定义,得出$m^2+16= (4-m)^2+1,$求出m的值,即可得出答案.
🔔关键提醒
本题主要考查了勾股定理、等腰三角形定义,熟练掌握勾股定理和正确计算是解题的关键.

答案： ($\frac{1}{8}$,0)　[解析]设D(m,0).
∵点A(0,4),点C(4,1),
∴AD²=m²+4²=m²+16,CD²=(4−m)²+1.由题意可知AD=CD,
∴AD²=CD²,
∴m²+16=(4−m)²+1,
∴m=$\frac{1}{8}$.故点D的坐标为($\frac{1}{8}$,0).

例8 如图,平面直角坐标系中四边形ABCD的面积是( ).


A.4
B.5.5
C.4.5
D.5
名师启发 过点A作x轴的垂线,垂足为E,将不规则四边形分割为两个直角三角形和一个直角梯形求其面积即可.
🌍归纳总结
本题考查了平面直角坐标系中不规则图形面积的求法,一般需要作x轴(y轴)的垂线,将原图形分割为可求面积的图形,再求其面积和.

答案： C　[解析]过点A作AE⊥BC,垂足为E,则S四边形ABCD=S△OCD+S梯形ODAE+S△ABE=$\frac{1}{2}$×1×1+$\frac{1}{2}$×(1+2)×2+$\frac{1}{2}$×1×2=4.5.故选C.