《2025年实验班提优训练八年级数学上册苏科版》

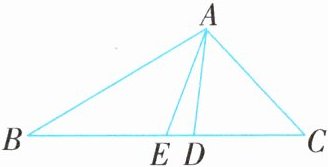
例2 (2025·西安雁塔区二模)如图,在△ABC中,AD是它的角平分线,AE是它的中线,AB= 5,AC= 3,BC= 7,则ED长为( ).


A.$\frac{15}{7}$
B.$\frac{7}{15}$
C.$\frac{7}{8}$
D.$\frac{8}{7}$
名师启发 过点D作DG⊥AB于点G,DH⊥AC于点H,根据角平分线上的点到角两边的距离相等得到DG= DH,根据三角形面积公式求出BD,再根据三角形的中线的概念求出BE,进而求出D
E.归纳总结
本题考查的是三角形的角平分线、中线和高,掌握三角形的中线的概念、角平分线的性质是解题的关键.

答案：
C [解析]如图，过点D作DG⊥AB于点G，DH⊥AC于点H.

∵AD平分∠BAC，DG⊥AB，DH⊥AC，
∴DG = DH，
∴$\frac{S_{\triangle BAD}}{S_{\triangle CAD}}=\frac{AB}{AC}=\frac{5}{3}$，
∴$\frac{BD}{DC}=\frac{5}{3}$.
∵BC = 7，
∴BD = $\frac{35}{8}$.
∵AE是△ABC的中线，BC = 7，
∴BE = $\frac{7}{2}$，
∴DE = BD - BE = $\frac{35}{8}-\frac{7}{2}=\frac{7}{8}$.故选C.

例3 一个三角形的三边长分别为3,5,a,另一个三角形的三边长分别为5,4,b,若这两个三角形全等,则a+b= ______.
名师启发 根据已知条件分清对应边,结合全等三角形的性质可得出答案.
归纳总结
本题考查了全等三角形性质的应用,能熟记全等三角形的性质是解题的关键.注意：全等三角形的对应边相等.

答案： 7 [解析]
∵一个三角形的三边长分别为3,5,a，另一个三角形的三边长分别为5,4,b，且这两个三角形全等，
∴a = 4，b = 3，
∴a + b = 7.

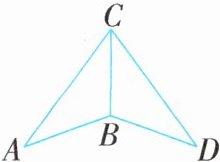
例4 (2025·宿迁期中)如图,△ABC≌△DBC,∠A= 34°,∠ACD= 72°,则∠DBC的度数是( ).


A.110°
B.105°
C.64°
D.100°
名师启发 根据全等三角形的性质求出∠D= ∠A= 34°,∠ABC= ∠DBC,∠ACB= ∠DCB,求出∠DCB,根据三角形内角和定理求出即可.
归纳总结
本题考查了全等三角形的性质的应用,能根据全等三角形的性质得出∠D= ∠A= 34°,∠ABC= ∠DBC,∠ACB= ∠DCB是解此题的关键.注意：全等三角形的对应角相等,对应边相等.

答案： A [解析]
∵△ABC≌△DBC，∠A = 34°，
∴∠D = ∠A = 34°，∠ABC = ∠DBC，∠ACB = ∠DCB.
∵∠ACD = 72°，
∴∠BCD = ∠ACB = 36°，
∴∠DBC = 180° - ∠D - ∠DCB = 110°.故选A.

例5 (2024·扬州广陵区期中)已知：△ABC≌△A'B'C',AD,A'D'分别是△ABC和△A'B'C'的高,求证：AD= A'D'.

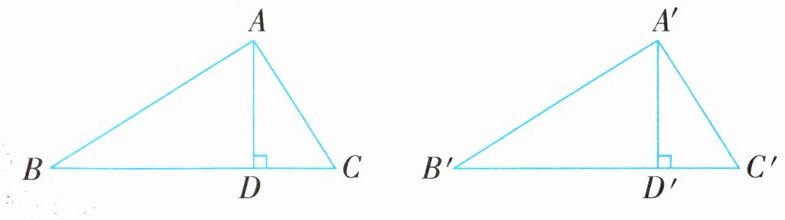
名师启发 由全等三角形的性质,得AB= A'B',∠B= ∠B'.又∠ADB= ∠A'D'B'= 90°,即可证明△ABD≌△A'B'D'(AAS),最终推出AD= A'D'.
归纳总结
本题考查了全等三角形的性质和判定方法,解题的关键是熟练掌握有关全等三角形的知识.全等三角形的性质：全等三角形对应边相等,对应角相等.

答案：
∵△ABC≌△A'B'C'，
∴AB = A'B'，∠B = ∠B'.
∵AD，A'D'分别是△ABC和△A'B'C'的高，
∴∠ADB = ∠A'D'B' = 90°，
∴△ABD≌△A'B'D'(AAS)，
∴AD = A'D'.