搜索
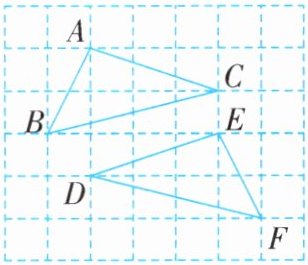
例3 (2024·陕西中考)如图,在6×7的网格中,每个小正方形的边长均为1,△ABC和△DFE的顶点都在格点上. 求证：∠ABC= ∠DFE.
名师启发 根据网格图中,每个小正方形的边长为1,得到两个三角形的每条边长,从而得到两个三角形对应边相等,因此两个三角形全等,根据全等三角形的性质,可得对应角相等,即可得到结果.
归纳总结
本题考查了勾股定理的应用.在网格图中,可通过勾股定理求三角形的边长.
名师启发 根据网格图中,每个小正方形的边长为1,得到两个三角形的每条边长,从而得到两个三角形对应边相等,因此两个三角形全等,根据全等三角形的性质,可得对应角相等,即可得到结果.
归纳总结
本题考查了勾股定理的应用.在网格图中,可通过勾股定理求三角形的边长.
答案：
如图,每个小正方形的边长均为1,$\because BC=\sqrt{4^{2}+1^{2}}=\sqrt{17}$,$DF=\sqrt{4^{2}+1^{2}}=\sqrt{17}$,$\therefore BC=DF$.同理可得 $DE=AC=\sqrt{10}$,$EF=AB=\sqrt{5}$.在$\triangle ABC$和$\triangle EFD$中,$\begin{cases} AB=EF, \\ BC=FD, \\ AC=ED, \end{cases}$$\therefore \triangle ABC\cong\triangle EFD(SSS)$,$\therefore \angle ABC=\angle DFE$.
例4 如图(1),美丽的弦图,蕴含着四个全等的直角三角形.
(1)弦图中包含了一大、一小两个正方形,已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c,结合图(1),试验证勾股定理；
(2)如图(2),将四个全等的直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC= 3,求该飞镖状图案的面积；
(3)如图(3),将八个全等的直角三角形紧密地拼接,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为$S_1,S_2,S_3$,若$S_1 + S_2 + S_3 = 16$,求$S_2$的值.
名师启发 (1)通过两种方式表示图中小正方形的面积证明勾股定理；(2)可设AC= x,根据勾股定理列出方程可求x,再根据直角三角形的面积公式计算即可求解；(3)根据图形的特征设出四边形MNKT的面积为x,将其余八个全等的三角形中一个面积设为y,从而用x,y表示出$S_1,S_2,S_3$,即可得出答案.
方法技巧
本题考查了勾股定理的证明与图形面积的关系,本题用数形结合来证明勾股定理,锻炼了学生数形结合的思想方法.
(1)弦图中包含了一大、一小两个正方形,已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c,结合图(1),试验证勾股定理；
(2)如图(2),将四个全等的直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC= 3,求该飞镖状图案的面积；
(3)如图(3),将八个全等的直角三角形紧密地拼接,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为$S_1,S_2,S_3$,若$S_1 + S_2 + S_3 = 16$,求$S_2$的值.
名师启发 (1)通过两种方式表示图中小正方形的面积证明勾股定理；(2)可设AC= x,根据勾股定理列出方程可求x,再根据直角三角形的面积公式计算即可求解；(3)根据图形的特征设出四边形MNKT的面积为x,将其余八个全等的三角形中一个面积设为y,从而用x,y表示出$S_1,S_2,S_3$,即可得出答案.方法技巧
本题考查了勾股定理的证明与图形面积的关系,本题用数形结合来证明勾股定理,锻炼了学生数形结合的思想方法.
答案：
(1)$S_{小正方形}=(a - b)^{2}=a^{2}-2ab + b^{2}$,$S_{小正方形}=c^{2}-4×\frac{1}{2}ab=c^{2}-2ab$,即 $a^{2}-2ab + b^{2}=c^{2}-2ab$,则 $a^{2}+b^{2}=c^{2}$.
(2)$24÷4 = 6$,设 $AC=x$,依题意,得$(x + 3)^{2}+3^{2}=(6 - x)^{2}$,解得 $x = 1$,则 $\frac{1}{2}×(3 + 1)×3×4=\frac{1}{2}×4×3×4 = 24$.故该飞镖状图案的面积是24.
(3)将四边形MTKN的面积设为x,将其余八个全等的三角形中的一个面积设为y.$\because$ 正方形ABCD、正方形EFGH、正方形MNKT的面积分别为$S_{1},S_{2},S_{3}$,$S_{1}+S_{2}+S_{3}=16$,$\therefore S_{1}=8y + x$,$S_{2}=4y + x$,$S_{3}=x$,$\therefore S_{1}+S_{2}+S_{3}=3x + 12y = 16$,$\therefore x + 4y=\frac{16}{3}$,$\therefore S_{2}=x + 4y=\frac{16}{3}$.
(1)$S_{小正方形}=(a - b)^{2}=a^{2}-2ab + b^{2}$,$S_{小正方形}=c^{2}-4×\frac{1}{2}ab=c^{2}-2ab$,即 $a^{2}-2ab + b^{2}=c^{2}-2ab$,则 $a^{2}+b^{2}=c^{2}$.
(2)$24÷4 = 6$,设 $AC=x$,依题意,得$(x + 3)^{2}+3^{2}=(6 - x)^{2}$,解得 $x = 1$,则 $\frac{1}{2}×(3 + 1)×3×4=\frac{1}{2}×4×3×4 = 24$.故该飞镖状图案的面积是24.
(3)将四边形MTKN的面积设为x,将其余八个全等的三角形中的一个面积设为y.$\because$ 正方形ABCD、正方形EFGH、正方形MNKT的面积分别为$S_{1},S_{2},S_{3}$,$S_{1}+S_{2}+S_{3}=16$,$\therefore S_{1}=8y + x$,$S_{2}=4y + x$,$S_{3}=x$,$\therefore S_{1}+S_{2}+S_{3}=3x + 12y = 16$,$\therefore x + 4y=\frac{16}{3}$,$\therefore S_{2}=x + 4y=\frac{16}{3}$.
查看更多完整答案，请扫码查看
