《2025年实验班提优训练八年级数学上册苏科版》

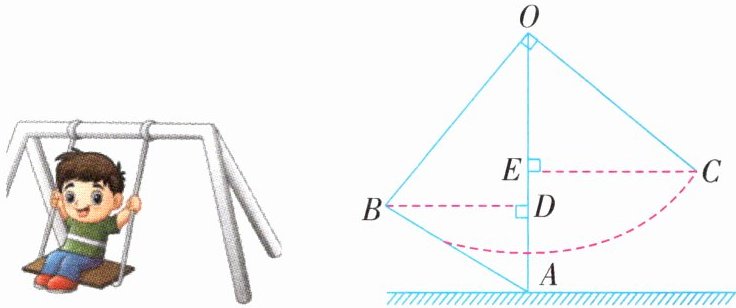
例6 (2025·盐城盐都区月考)小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面0.8m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD,CE分别为1.4m和2m,∠BOC= 90°.
(1)△OBD与△COE全等吗？请说明理由.
(2)小明的爸爸是在距离地面多高的地方接住小明的？

名师启发 (1)先证明∠COE= ∠OBD,再根据AAS即可证明结论；
(2)由△COE≌△OBD,得出CE= OD,OE= BD,即可推出结果.
关键提醒
本题考查了三角形全等的判定方法,判定两个三角形全等的一般方法有SSS,SAS,ASA,AAS,HL.注意：AAA和SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与.

答案：
(1)△OBD与△COE全等.理由如下：由题意可知∠CEO = ∠BDO = 90°，BO = CO，∠BOC = 90°，
∴∠COE + ∠BOD = ∠BOD + ∠OBD = 90°，
∴∠COE = ∠OBD.
在△COE和△OBD中，$\begin{cases} ∠COE = ∠OBD, \\ ∠OEC = ∠BDO, \\ OC = BO, \end{cases}$
∴△COE≌△OBD(AAS).
(2)
∵△COE≌△OBD，
∴CE = OD，OE = BD.
又BD，CE分别为1.4m和2m，
∴DE = OD - OE = CE - BD = 2 - 1.4 = 0.6(m)，
∴AE = DE + AD = 0.6 + 0.8 = 1.4(m).故小明的爸爸是在距离地面1.4m处接住小明的.

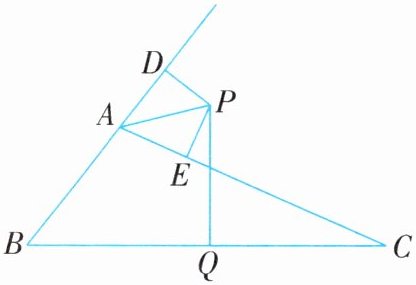
例7 (2025·无锡锡山区期中)如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥BD于点D,PE⊥AC于点E.
(1)求证：BD= CE；
(2)若AB= 6cm,AC= 10cm,求AD的长.

名师启发 (1)连接BP,CP,根据线段垂直平分线上的点到两端点的距离相等可得BP= CP,根据角平分线上的点到角的两边距离相等可得DP= EP,然后利用“HL”证明Rt△BDP和Rt△CEP全等,根据全等三角形对应边相等证明即可；
(2)利用“HL”证明Rt△ADP和Rt△AEP全等,根据全等三角形对应边相等可得AD= AE,再根据AB,AC的长度表示出AD,CE,然后解方程即可.
归纳总结
在使用线段的垂直平分线的性质及其判定时要注意它们的区别：性质是“已知点在垂直平分线上”,结论是“线段相等”；判定正好相反,它们是一对互逆定理.

答案：
(1)连接BP，CP，
∵点P在BC的垂直平分线上，
∴BP = CP.
∵AP是∠DAC的平分线，
∴DP = EP.
在Rt△BDP和Rt△CEP中，$\begin{cases} BP = CP, \\ DP = EP, \end{cases}$
∴Rt△BDP≌Rt△CEP(HL)，
∴BD = CE.
(2)在Rt△ADP和Rt△AEP中，$\begin{cases} AP = AP, \\ DP = EP, \end{cases}$
∴Rt△ADP≌Rt△AEP(HL)，
∴AD = AE.
∵AB = 6cm，AC = 10cm，
∴6 + AD = 10 - AE，即6 + AD = 10 - AD，解得AD = 2cm.