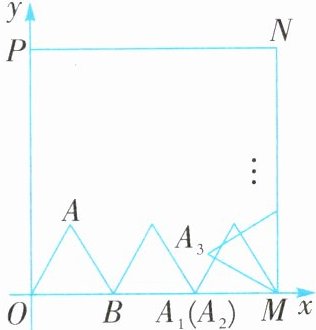
例11 (2024·黑龙江中考)如图,在平面直角坐标系中,正方形OMNP顶点M的坐标为(3,0),△OAB是等边三角形,点B的坐标是(1,0),△OAB在正方形OMNP内部紧靠正方形OMNP的边(方向为O→M→N→P→O→M→…)做无滑动滚动,第一次滚动后,点A的对应点记为A_1,A_1的坐标是(2,0);第二次滚动后,A_1的对应点记为A_2,A_2的坐标是(2,0);第三次滚动后,A_2的对应点记为A_3,A_3的坐标是$(3-\frac{\sqrt{3}}{2},\frac{1}{2})$,如此下去,…,则A_2₀_2_4的坐标是______.
名师启发 根据点的坐标变化特点,找到变化规律,再计算求解.
🔔关键提醒
本题关键是得到该位置点的横、纵坐标的变化规律(Aₙ的坐标每12个循环一次).

名师启发 根据点的坐标变化特点,找到变化规律,再计算求解.
🔔关键提醒
本题关键是得到该位置点的横、纵坐标的变化规律(Aₙ的坐标每12个循环一次).
答案:
(1,3) [解析]由题知,点A₁的坐标为(2,0),点A₂的坐标为(2,0),点A₃的坐标为(3−$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),点A₄的坐标为(3,2),点A₅的坐标为(3,2),点A₆的坐标为($\frac{5}{2}$,3−$\frac{\sqrt{3}}{2}$),点A₇的坐标为(1,3),点A₈的坐标为(1,3),点A₉的坐标为($\frac{\sqrt{3}}{2}$,$\frac{5}{2}$),点A₁₀的坐标为(0,1),点A₁₁的坐标为(0,1),点A₁₂的坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),点A₁₃的坐标为(2,0),由此可见,点Aₙ的坐标每12个循环一次,因为2024÷12=168……8,所以点A₂₀₂₄的坐标为(1,3).
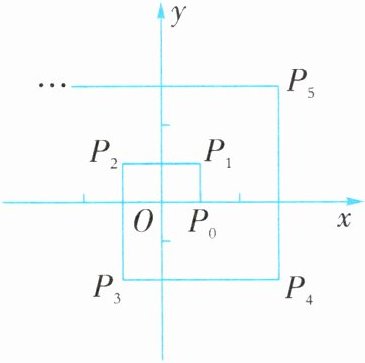
例12 如图,在平面直角坐标系中,设一动点M自P₀(1,0)处向上运动1个单位长度至$P_1(1,1),$然后向左运动2个单位长度至$P_2$处,再向下运动3个单位长度至$P_3$处,再向右运动4个单位长度至$P_4$处,再向上运动5个单位长度至$P_5$处,…,如此继续运动下去,设Pₙ(xₙ,yₙ),n= 1,2,3,…,则$x_1+x_2+…+x_9_9+x_1₀₀= ______.$
名师启发 根据各象限中点的特征,探究规律,利用规律解决问题.
🔔关键提醒
本题考查坐标与图形变化—平移,规律型问题,解题的关键是学会探究规律的方法,属于中考常考题型.

名师启发 根据各象限中点的特征,探究规律,利用规律解决问题.
🔔关键提醒
本题考查坐标与图形变化—平移,规律型问题,解题的关键是学会探究规律的方法,属于中考常考题型.
答案:
50 [解析]x₁+x₂+x₃+x₄=1−1−1+3=2;x₅+x₆+x₇+x₈=3−3−3+5=2;…;x₉₇+x₉₈+x₉₉+x₁₀₀=2,
∴原式=2×(100÷4)=50.
∴原式=2×(100÷4)=50.
例1 点P(2m-1,3)不在第二象限,则m的取值范围是( ).
A.$m>\frac{1}{2}$
B.$m\geq\frac{1}{2}$
C.$m<\frac{1}{2}$
D.$m\leq\frac{1}{2}$
解析 分清象限与坐标轴之间的关系即可解答.
答案 B
辨析归纳
任何一个象限不含坐标轴,坐标轴上的点不属于任何一个象限.
A.$m>\frac{1}{2}$
B.$m\geq\frac{1}{2}$
C.$m<\frac{1}{2}$
D.$m\leq\frac{1}{2}$
解析 分清象限与坐标轴之间的关系即可解答.
答案 B
辨析归纳
任何一个象限不含坐标轴,坐标轴上的点不属于任何一个象限.
答案:
B
例2 已知第四象限内的点P到x轴的距离为3,到y轴的距离为8,试确定点P的坐标.
解答 ∵点P在第四象限内,
∴点P的横坐标大于0,纵坐标小于0.
∵点P到x轴的距离是3,到y轴的距离是8,
∴点P的横坐标是8,纵坐标是-3,即点P的坐标为(8,-3).
辨析归纳
本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值是解题的关键.
解答 ∵点P在第四象限内,
∴点P的横坐标大于0,纵坐标小于0.
∵点P到x轴的距离是3,到y轴的距离是8,
∴点P的横坐标是8,纵坐标是-3,即点P的坐标为(8,-3).
辨析归纳
本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值是解题的关键.
答案:
∵点P在第四象限内,
∴点P的横坐标大于0,纵坐标小于0。
∵点P到x轴的距离是3,到y轴的距离是8,
∴点P的横坐标是8,纵坐标是-3,即点P的坐标为(8,-3)。
∵点P在第四象限内,
∴点P的横坐标大于0,纵坐标小于0。
∵点P到x轴的距离是3,到y轴的距离是8,
∴点P的横坐标是8,纵坐标是-3,即点P的坐标为(8,-3)。
例3 已知△ABC三个顶点的坐标分别为A(-3,0),B(1,4),C(5,0),试判断△ABC的形状.
解答 在△ABC中,
$AB^2= (1+3)^2+4^2= 32, $
$BC^2= (5-1)^2+4^2= 32, $
AC= 5-(-3)= 8,
∴$AB^2= BC^2,AC^2= 64, $
∴AB= BC且$AB^2+BC^2= AC^2, $
∴△ABC是等腰直角三角形.
辨析归纳
三角形的两边相等时,除了是等腰三角形外,还可能是特殊的等边三角形或等腰直角三角形.
解答 在△ABC中,
$AB^2= (1+3)^2+4^2= 32, $
$BC^2= (5-1)^2+4^2= 32, $
AC= 5-(-3)= 8,
∴$AB^2= BC^2,AC^2= 64, $
∴AB= BC且$AB^2+BC^2= AC^2, $
∴△ABC是等腰直角三角形.
辨析归纳
三角形的两边相等时,除了是等腰三角形外,还可能是特殊的等边三角形或等腰直角三角形.
答案:
在△ABC中,
$AB^2 = (1 + 3)^2 + 4^2 = 16 + 16 = 32$
$BC^2 = (5 - 1)^2 + 4^2 = 16 + 16 = 32$
$AC = 5 - (-3) = 8$
$AC^2 = 8^2 = 64$
∵ $AB^2 = BC^2$ 且 $AB^2 + BC^2 = AC^2$
∴ $AB = BC$ 且 △ABC是直角三角形
∴ △ABC是等腰直角三角形
$AB^2 = (1 + 3)^2 + 4^2 = 16 + 16 = 32$
$BC^2 = (5 - 1)^2 + 4^2 = 16 + 16 = 32$
$AC = 5 - (-3) = 8$
$AC^2 = 8^2 = 64$
∵ $AB^2 = BC^2$ 且 $AB^2 + BC^2 = AC^2$
∴ $AB = BC$ 且 △ABC是直角三角形
∴ △ABC是等腰直角三角形
查看更多完整答案,请扫码查看


