例7 如图,在△ABC中,AD= 12,BD= 5,CD= 16,AC= 20,求△ABC的周长.

名师启发 先根据勾股定理的逆定理得出△ADC是直角三角形,再根据勾股定理求出AB,最后求出△ABC的周长.
关键提醒
本题主要考查了勾股定理及其逆定理,在任何一个直角三角形中,两条直角边长的平方和一定等于斜边长的平方.正确判断出△ADC是直角三角形是解题关键.

名师启发 先根据勾股定理的逆定理得出△ADC是直角三角形,再根据勾股定理求出AB,最后求出△ABC的周长.
关键提醒
本题主要考查了勾股定理及其逆定理,在任何一个直角三角形中,两条直角边长的平方和一定等于斜边长的平方.正确判断出△ADC是直角三角形是解题关键.
答案:
$\because AD = 12$,$CD = 16$,$AC = 20$,$\therefore AD^{2}+CD^{2}=AC^{2}$,$\therefore \triangle ADC$是直角三角形,且$\angle ADC = 90^{\circ}$.$\because BD = 5$,$\therefore BC = BD + CD = 5 + 16 = 21$.$\because \angle ADB=\angle ADC = 90^{\circ}$,$\therefore AB^{2}=AD^{2}+BD^{2}=12^{2}+5^{2}=13^{2}$,$\therefore AB = 13$,$\therefore \triangle ABC$的周长是$AB + BC + AC = 13 + 21 + 20 = 54$.
例8 (2024·连云港赣榆区期中)如图,在△ABC中,AB边上的垂直平分线DE与AB,AC分别交于点E和D,且$CB^2 = AD^2 - CD^2$.
(1)求证:∠C= 90°;
(2)若AC= 4,BC= 3,求CD的长.

名师启发 (1)连接BD,根据线段垂直平分线的性质和勾股定理的逆定理即可证明;
(2)设CD= x,则AD= BD= 4-x,在Rt△BCD中,根据$BD^2 - CD^2 = BC^2$,列出方程计算即可求解.
归纳总结
本题考查了线段垂直平分线的性质,勾股定理的逆定理,应注意方程思想的运用.
(1)求证:∠C= 90°;
(2)若AC= 4,BC= 3,求CD的长.

名师启发 (1)连接BD,根据线段垂直平分线的性质和勾股定理的逆定理即可证明;
(2)设CD= x,则AD= BD= 4-x,在Rt△BCD中,根据$BD^2 - CD^2 = BC^2$,列出方程计算即可求解.
归纳总结
本题考查了线段垂直平分线的性质,勾股定理的逆定理,应注意方程思想的运用.
答案:
(1)如图,连接BD.$\because$ AB边上的垂直平分线为DE,$\therefore AD = BD$.$\because CB^{2}=AD^{2}-CD^{2}$,$\therefore CB^{2}=BD^{2}-CD^{2}$,$\therefore CB^{2}+CD^{2}=BD^{2}$,$\therefore \angle C = 90^{\circ}$.
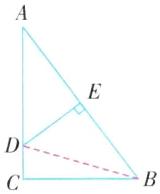
(2)设 $CD = x$,则 $AD = BD = 4 - x$,在$Rt\triangle BCD$中,$BD^{2}-CD^{2}=BC^{2}$,$\therefore (4 - x)^{2}-x^{2}=3^{2}$,解得 $x=\frac{7}{8}$,$\therefore CD$的长为$\frac{7}{8}$.
(1)如图,连接BD.$\because$ AB边上的垂直平分线为DE,$\therefore AD = BD$.$\because CB^{2}=AD^{2}-CD^{2}$,$\therefore CB^{2}=BD^{2}-CD^{2}$,$\therefore CB^{2}+CD^{2}=BD^{2}$,$\therefore \angle C = 90^{\circ}$.

(2)设 $CD = x$,则 $AD = BD = 4 - x$,在$Rt\triangle BCD$中,$BD^{2}-CD^{2}=BC^{2}$,$\therefore (4 - x)^{2}-x^{2}=3^{2}$,解得 $x=\frac{7}{8}$,$\therefore CD$的长为$\frac{7}{8}$.
例9 (2024·巴中中考)“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深几何?”这是我国数学史上的“葭生池中”问题,即AC= 5,DC= 1,BD= BA,则BC= ( ).

A.8
B.10
C.12
D.13
名师启发 设BC= x,则BD= BA= x+1,在Rt△ABC中,由勾股定理得出方程求解即可.
归纳总结
本题考查了勾股定理的应用,勾股定理描述了直角三角形的三条边之间存在的等量关系,根据它就可以把问题转化为解方程的问题.

A.8
B.10
C.12
D.13
名师启发 设BC= x,则BD= BA= x+1,在Rt△ABC中,由勾股定理得出方程求解即可.
归纳总结
本题考查了勾股定理的应用,勾股定理描述了直角三角形的三条边之间存在的等量关系,根据它就可以把问题转化为解方程的问题.
答案:
C [解析]设 $BC = x$,则 $BD = BA = x + 1$,在$Rt\triangle ABC$中,由勾股定理,得$AB^{2}=AC^{2}+BC^{2}$,即 $(x + 1)^{2}=5^{2}+x^{2}$,解得 $x = 12$,即 $BC = 12$.故选C.
查看更多完整答案,请扫码查看


