3. 一个三角形有两边长分别为15和20,第三边上的高为12,则第三边的长为( ).
A.7
B.25
C.16
D.7或25
A.7
B.25
C.16
D.7或25
答案:
D [解析]当第三边上的高在三角形内部时,如图
(1)所示,$AB = 20$,$AC = 15$,$AD = 12$.$\because AD$是高,$\therefore \triangle ABD$,$\triangle ACD$是直角三角形,$\therefore BD^{2}=AB^{2}-AD^{2}=20^{2}-12^{2}=256$,$\therefore BD = 16$.同理可得 $CD = 9$,$\therefore BC = BD + CD = 16 + 9 = 25$;

当第三边上的高在三角形外部时,如图
(2)所示,$AB = 20$,$AC = 15$,$AD = 12$.$\because AD$是高,$\therefore \triangle ABD$,$\triangle ACD$是直角三角形,$\therefore BD^{2}=AB^{2}-AD^{2}=20^{2}-12^{2}=256$,$\therefore BD = 16$.同理可得 $CD = 9$,$\therefore BC = BD - CD = 16 - 9 = 7$.综上所述,第三边的长为25或7.
D [解析]当第三边上的高在三角形内部时,如图
(1)所示,$AB = 20$,$AC = 15$,$AD = 12$.$\because AD$是高,$\therefore \triangle ABD$,$\triangle ACD$是直角三角形,$\therefore BD^{2}=AB^{2}-AD^{2}=20^{2}-12^{2}=256$,$\therefore BD = 16$.同理可得 $CD = 9$,$\therefore BC = BD + CD = 16 + 9 = 25$;

当第三边上的高在三角形外部时,如图
(2)所示,$AB = 20$,$AC = 15$,$AD = 12$.$\because AD$是高,$\therefore \triangle ABD$,$\triangle ACD$是直角三角形,$\therefore BD^{2}=AB^{2}-AD^{2}=20^{2}-12^{2}=256$,$\therefore BD = 16$.同理可得 $CD = 9$,$\therefore BC = BD - CD = 16 - 9 = 7$.综上所述,第三边的长为25或7.
4. (2025·苏州工业园区期中改编)在△ABC中,AB= 25,AC= 17,BC上的高AD长为15,则△ABC的面积为______.
答案:
210或90 [解析]当$\triangle ABC$为锐角三角形时,如图
(1)所示,$AB = 25$,$AC = 17$,$AD\perp BC$,$AD = 15$,在$Rt\triangle ABD$中,$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{25^{2}-15^{2}}=20$,在$Rt\triangle ACD$中,$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{17^{2}-15^{2}}=8$,$\therefore BC = BD + CD = 20 + 8 = 28$,$\therefore S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}×28×15 = 210$;

②当$\triangle ABC$为钝角三角形时,如图
(2)所示,在$Rt\triangle ABD$中,$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{25^{2}-15^{2}}=20$,在$Rt\triangle ACD$中,$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{17^{2}-15^{2}}=8$,$\therefore BC = BD - CD = 20 - 8 = 12$,$\therefore S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}×12×15 = 90$.综上所述,$\triangle ABC$的面积为210或90.
210或90 [解析]当$\triangle ABC$为锐角三角形时,如图
(1)所示,$AB = 25$,$AC = 17$,$AD\perp BC$,$AD = 15$,在$Rt\triangle ABD$中,$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{25^{2}-15^{2}}=20$,在$Rt\triangle ACD$中,$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{17^{2}-15^{2}}=8$,$\therefore BC = BD + CD = 20 + 8 = 28$,$\therefore S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}×28×15 = 210$;

②当$\triangle ABC$为钝角三角形时,如图
(2)所示,在$Rt\triangle ABD$中,$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{25^{2}-15^{2}}=20$,在$Rt\triangle ACD$中,$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{17^{2}-15^{2}}=8$,$\therefore BC = BD - CD = 20 - 8 = 12$,$\therefore S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}×12×15 = 90$.综上所述,$\triangle ABC$的面积为210或90.
传统文化
例1 清代扬州数学家罗士琳痴迷研究勾股定理,提出推算勾股数的“罗士琳法则”.其中有一个法则是“如果k是大于2的偶数,那么k、k的一半的平方减1、k的一半的平方加1是一组勾股数.”
(1)按照这个法则,写出2组不同的勾股数______,______;(最大数不超过18)
(2)用等式表示这三个勾股数的数量关系并证明.
解析 (1)分别令k= 4、k= 6,再求出其余的数即可;
(2)分别用k表示出一组勾股数,再找出其数量关系即可.
答案 (1)3,4,5 6,8,10(答案不唯一)
(2)当k大于2时,$k^2 + [(\frac{1}{2}k)^2 - 1]^2 = [(\frac{1}{2}k)^2 + 1]^2$.证明如下:
∵左边$=k^2 + [(\frac{1}{2}k)^2 - 1]^2 = k^2 + (\frac{1}{4}k^2 - 1)^2 = k^2 + \frac{1}{16}k^4 + 1 - \frac{1}{2}k^2 = \frac{1}{16}k^4 + \frac{1}{2}k^2 + 1$;
右边$=[(\frac{1}{2}k)^2 + 1]^2 = (\frac{1}{4}k^2 + 1)^2 = \frac{1}{16}k^4 + \frac{1}{2}k^2 + 1$,∴左边= 右边,∴等式成立.
点拨
本题考查的是勾股数,熟知满足$a^2 + b^2 = c^2$的三个正整数称为勾股数是解答此题的关键.
例1 清代扬州数学家罗士琳痴迷研究勾股定理,提出推算勾股数的“罗士琳法则”.其中有一个法则是“如果k是大于2的偶数,那么k、k的一半的平方减1、k的一半的平方加1是一组勾股数.”
(1)按照这个法则,写出2组不同的勾股数______,______;(最大数不超过18)
(2)用等式表示这三个勾股数的数量关系并证明.
解析 (1)分别令k= 4、k= 6,再求出其余的数即可;
(2)分别用k表示出一组勾股数,再找出其数量关系即可.
答案 (1)3,4,5 6,8,10(答案不唯一)
(2)当k大于2时,$k^2 + [(\frac{1}{2}k)^2 - 1]^2 = [(\frac{1}{2}k)^2 + 1]^2$.证明如下:
∵左边$=k^2 + [(\frac{1}{2}k)^2 - 1]^2 = k^2 + (\frac{1}{4}k^2 - 1)^2 = k^2 + \frac{1}{16}k^4 + 1 - \frac{1}{2}k^2 = \frac{1}{16}k^4 + \frac{1}{2}k^2 + 1$;
右边$=[(\frac{1}{2}k)^2 + 1]^2 = (\frac{1}{4}k^2 + 1)^2 = \frac{1}{16}k^4 + \frac{1}{2}k^2 + 1$,∴左边= 右边,∴等式成立.
点拨
本题考查的是勾股数,熟知满足$a^2 + b^2 = c^2$的三个正整数称为勾股数是解答此题的关键.
答案:
(1)
当$k = 4$时,$\frac{k}{2}=2$,$\frac{k}{2}^2 - 1 = 3$,$\frac{k}{2}^2 + 1 = 5$,得到勾股数$3$,$4$,$5$;
当$k = 6$时,$\frac{k}{2}=3$,$\frac{k}{2}^2 - 1 = 8$,$\frac{k}{2}^2 + 1 = 10$,得到勾股数$6$,$8$,$10$。
故答案为$3$,$4$,$5$;$6$,$8$,$10$。
(2)
这三个勾股数的数量关系为$k^2+[(\frac{1}{2}k)^2 - 1]^2=[(\frac{1}{2}k)^2 + 1]^2$。
证明:
左边$=k^2 + [(\frac{1}{2}k)^2 - 1]^2=k^2+(\frac{1}{4}k^2 - 1)^2=k^2+\frac{1}{16}k^4 + 1-\frac{1}{2}k^2=\frac{1}{16}k^4+\frac{1}{2}k^2 + 1$;
右边$= [(\frac{1}{2}k)^2 + 1]^2=(\frac{1}{4}k^2 + 1)^2=\frac{1}{16}k^4+\frac{1}{2}k^2 + 1$。
所以左边$=$右边,等式成立。
(1)
当$k = 4$时,$\frac{k}{2}=2$,$\frac{k}{2}^2 - 1 = 3$,$\frac{k}{2}^2 + 1 = 5$,得到勾股数$3$,$4$,$5$;
当$k = 6$时,$\frac{k}{2}=3$,$\frac{k}{2}^2 - 1 = 8$,$\frac{k}{2}^2 + 1 = 10$,得到勾股数$6$,$8$,$10$。
故答案为$3$,$4$,$5$;$6$,$8$,$10$。
(2)
这三个勾股数的数量关系为$k^2+[(\frac{1}{2}k)^2 - 1]^2=[(\frac{1}{2}k)^2 + 1]^2$。
证明:
左边$=k^2 + [(\frac{1}{2}k)^2 - 1]^2=k^2+(\frac{1}{4}k^2 - 1)^2=k^2+\frac{1}{16}k^4 + 1-\frac{1}{2}k^2=\frac{1}{16}k^4+\frac{1}{2}k^2 + 1$;
右边$= [(\frac{1}{2}k)^2 + 1]^2=(\frac{1}{4}k^2 + 1)^2=\frac{1}{16}k^4+\frac{1}{2}k^2 + 1$。
所以左边$=$右边,等式成立。
1. (2025·无锡江阴期末)我国古代称直角三角形为“勾股形”.如图,数学家刘徽(约公元225年—公元295年)将勾股形分割成一个正方形和两对全等的直角三角形.若a= 10,b= 2,则此勾股形的面积为( ).

A.28
B.30
C.32
D.36

A.28
B.30
C.32
D.36
答案:
B [解析]设阴影部分的直角三角形的未知边长为x,则 $BC = x + b$,$AC = x + a$,$BA = a + b$,由勾股定理得$(x + b)^{2}+(a + b)^{2}=(x + a)^{2}$.
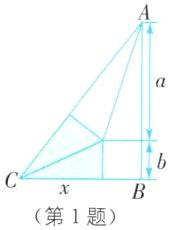
$\because a = 10$,$b = 2$,$\therefore (x + 2)^{2}+(10 + 2)^{2}=(x + 10)^{2}$,解得 $x = 3$,$\therefore BC = 3 + 2 = 5$,$AB = 10 + 2 = 12$,$\therefore \triangle ABC$的面积$=\frac{1}{2}×12×5 = 30$.故选B.
B [解析]设阴影部分的直角三角形的未知边长为x,则 $BC = x + b$,$AC = x + a$,$BA = a + b$,由勾股定理得$(x + b)^{2}+(a + b)^{2}=(x + a)^{2}$.

$\because a = 10$,$b = 2$,$\therefore (x + 2)^{2}+(10 + 2)^{2}=(x + 10)^{2}$,解得 $x = 3$,$\therefore BC = 3 + 2 = 5$,$AB = 10 + 2 = 12$,$\therefore \triangle ABC$的面积$=\frac{1}{2}×12×5 = 30$.故选B.
新情境
例2 (2025·镇江丹徒区期中)随着中国科技、经济的不断发展,5G信号的覆盖的广泛性和稳定性都有更好的表现.如图,有一辆汽车沿直线AB方向,由点A向点B行驶,已知点C为某个5G信号源,且点C到点A和点B的距离分别为60 m和80 m,且AB= 100 m,信号源中心周围50 m及以内可以接收到5G信号.
(1)汽车在从点A向点B行驶的过程中,能接收到5G信号吗?为什么?
(2)若汽车的速度为10 m/s,请问有多长时间可以接收到5G信号?
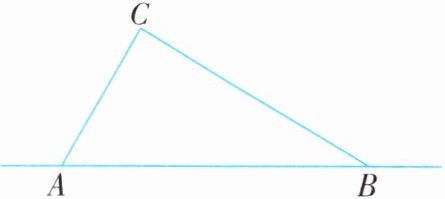
解析 (1)过点C作CD⊥AB于点D,由AC,BC,AB的长,可得出$AC^2 + BC^2 = AB^2$,进而可得出∠ACB= 90°,再结合三角形的面积公式,即可求出CD的长,由该值小于50 m,即可得出汽车在从点A向点B行驶的过程中,能接收到5G信号;
(2)设点E,F在直线AB上,且CE= CF= 50 m,利用勾股定理,可求出DE的长,进而可得出DF,EF的长,再利用时间= 路程÷速度,即可求出结论.
答案 (1)汽车在从点A向点B行驶的过程中,能接收到5G信号,理由如下:
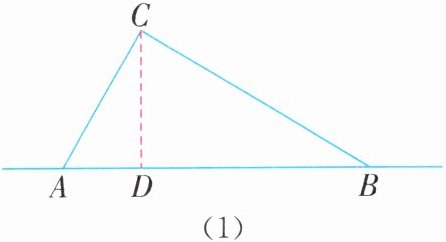
过点C作CD⊥AB于点D,如图(1)所示.
∵AC= 60 m,BC= 80 m,AB= 100 m,$60^2 + 80^2 = 100^2$,
∴$AC^2 + BC^2 = AB^2$,∴∠ACB= 90°,
∴$CD = \frac{\frac{1}{2}AC·BC}{\frac{1}{2}AB} = \frac{\frac{1}{2}×60×80}{\frac{1}{2}×100} = 48(m)$.
∵48 m<50 m,
∴汽车在从点A向点B行驶的过程中,能接收到5G信号.
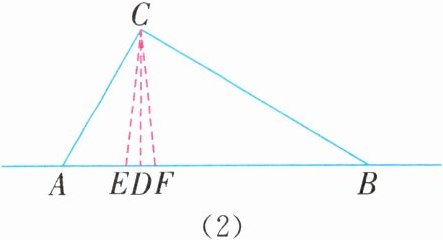
(2)设点E,F在直线AB上,且CE= CF= 50 m,如图(2)所示.
在Rt△CDE中,CD= 48 m,CE= 50 m,
∴$DE = \sqrt{CE^2 - CD^2} = \sqrt{50^2 - 48^2} = 14(m)$,
同理DF= DE= 14 m,
∴EF= DE + DF= 14 + 14= 28(m),
∴28÷10= 2.8(s).
故有2.8 s可以接收到5G信号.
点拨
本题考查了勾股定理的应用、勾股定理的逆定理以及三角形的面积,解题的关键是:(1)利用面积法,求出点C到AB的距离;(2)利用勾股定理,求出在直线AB上能接收到5G信号的长度.
例2 (2025·镇江丹徒区期中)随着中国科技、经济的不断发展,5G信号的覆盖的广泛性和稳定性都有更好的表现.如图,有一辆汽车沿直线AB方向,由点A向点B行驶,已知点C为某个5G信号源,且点C到点A和点B的距离分别为60 m和80 m,且AB= 100 m,信号源中心周围50 m及以内可以接收到5G信号.
(1)汽车在从点A向点B行驶的过程中,能接收到5G信号吗?为什么?
(2)若汽车的速度为10 m/s,请问有多长时间可以接收到5G信号?

解析 (1)过点C作CD⊥AB于点D,由AC,BC,AB的长,可得出$AC^2 + BC^2 = AB^2$,进而可得出∠ACB= 90°,再结合三角形的面积公式,即可求出CD的长,由该值小于50 m,即可得出汽车在从点A向点B行驶的过程中,能接收到5G信号;
(2)设点E,F在直线AB上,且CE= CF= 50 m,利用勾股定理,可求出DE的长,进而可得出DF,EF的长,再利用时间= 路程÷速度,即可求出结论.
答案 (1)汽车在从点A向点B行驶的过程中,能接收到5G信号,理由如下:
过点C作CD⊥AB于点D,如图(1)所示.
∵AC= 60 m,BC= 80 m,AB= 100 m,$60^2 + 80^2 = 100^2$,
∴$AC^2 + BC^2 = AB^2$,∴∠ACB= 90°,
∴$CD = \frac{\frac{1}{2}AC·BC}{\frac{1}{2}AB} = \frac{\frac{1}{2}×60×80}{\frac{1}{2}×100} = 48(m)$.
∵48 m<50 m,
∴汽车在从点A向点B行驶的过程中,能接收到5G信号.
(2)设点E,F在直线AB上,且CE= CF= 50 m,如图(2)所示.
在Rt△CDE中,CD= 48 m,CE= 50 m,
∴$DE = \sqrt{CE^2 - CD^2} = \sqrt{50^2 - 48^2} = 14(m)$,
同理DF= DE= 14 m,
∴EF= DE + DF= 14 + 14= 28(m),
∴28÷10= 2.8(s).
故有2.8 s可以接收到5G信号.


点拨
本题考查了勾股定理的应用、勾股定理的逆定理以及三角形的面积,解题的关键是:(1)利用面积法,求出点C到AB的距离;(2)利用勾股定理,求出在直线AB上能接收到5G信号的长度.
答案:
(1)汽车在从点$A$向点$B$行驶的过程中,能接收到$5G$信号,理由如下:
过点$C$作$CD \perp AB$于点$D$。
$\because AC = 60m$,$BC = 80m$,$AB = 100m$,$60^{2}+80^{2}=100^{2}$,
$\therefore AC^{2}+BC^{2}=AB^{2}$,$\therefore \angle ACB = 90^{\circ}$,
$\therefore CD=\frac{\frac{1}{2}AC\cdot BC}{\frac{1}{2}AB}=\frac{\frac{1}{2}×60×80}{\frac{1}{2}×100}=48(m)$。
$\because 48m < 50m$,
$\therefore$汽车在从点$A$向点$B$行驶的过程中,能接收到$5G$信号。
(2)设点$E$,$F$在直线$AB$上,且$CE = CF = 50m$。
在$Rt\triangle CDE$中,$CD = 48m$,$CE = 50m$,
$\therefore DE=\sqrt{CE^{2}-CD^{2}}=\sqrt{50^{2}-48^{2}} = 14(m)$,
同理$DF = DE = 14m$,
$\therefore EF=DE + DF=14 + 14 = 28(m)$,
$\therefore 28÷10 = 2.8(s)$。
故有$2.8s$可以接收到$5G$信号。
过点$C$作$CD \perp AB$于点$D$。
$\because AC = 60m$,$BC = 80m$,$AB = 100m$,$60^{2}+80^{2}=100^{2}$,
$\therefore AC^{2}+BC^{2}=AB^{2}$,$\therefore \angle ACB = 90^{\circ}$,
$\therefore CD=\frac{\frac{1}{2}AC\cdot BC}{\frac{1}{2}AB}=\frac{\frac{1}{2}×60×80}{\frac{1}{2}×100}=48(m)$。
$\because 48m < 50m$,
$\therefore$汽车在从点$A$向点$B$行驶的过程中,能接收到$5G$信号。
(2)设点$E$,$F$在直线$AB$上,且$CE = CF = 50m$。
在$Rt\triangle CDE$中,$CD = 48m$,$CE = 50m$,
$\therefore DE=\sqrt{CE^{2}-CD^{2}}=\sqrt{50^{2}-48^{2}} = 14(m)$,
同理$DF = DE = 14m$,
$\therefore EF=DE + DF=14 + 14 = 28(m)$,
$\therefore 28÷10 = 2.8(s)$。
故有$2.8s$可以接收到$5G$信号。
查看更多完整答案,请扫码查看


