《2025年启东中学作业本八年级数学上册苏科版盐城专版》

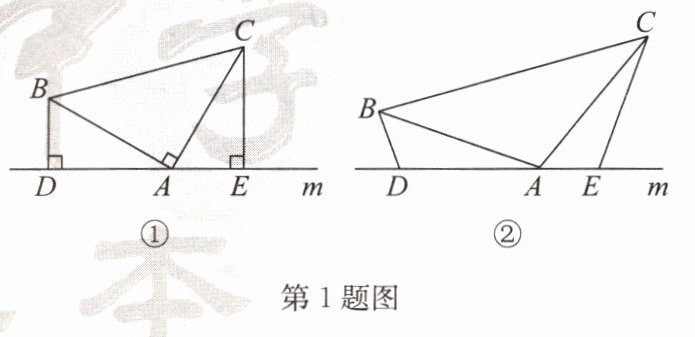
1.问题背景:(1)如图①,在$△ABC$中,$∠BAC= 90^{\circ },AB= AC$,直线m经过点A,$BD⊥$直线m,$CE⊥$直线m,垂足分别为D,E,求证:$DE= BD+CE;$
拓展延伸:(2)如图②,将(1)中的条件改为:在$△ABC$中,$AB= AC$,D,A,E三点都在直线m上,且$∠BDA= ∠AEC= ∠BAC$.请写出DE,BD,CE三条线段的数量关系,并说明理由.

答案： 1. （1）证明：
因为$BD\perp$直线$m$，$CE\perp$直线$m$，所以$\angle BDA=\angle AEC = 90^{\circ}$。
又因为$\angle BAC = 90^{\circ}$，所以$\angle BAD+\angle CAE=90^{\circ}$。
而$\angle BAD+\angle ABD = 90^{\circ}$，所以$\angle CAE=\angle ABD$。
在$\triangle ABD$和$\triangle CAE$中：
$\begin{cases}\angle BDA=\angle AEC\\\angle ABD=\angle CAE\\AB = AC\end{cases}$
根据$AAS$（两角及其中一角的对边对应相等的两个三角形全等），可得$\triangle ABD\cong\triangle CAE$。
所以$BD = AE$，$AD = CE$。
因为$DE=AD + AE$，所以$DE=BD + CE$。
2. （2）$DE = BD+CE$。
理由：
因为$\angle BDA=\angle BAC=\alpha$，所以$\angle DBA+\angle BAD=\angle BAD+\angle CAE = 180^{\circ}-\alpha$。
所以$\angle DBA=\angle CAE$。
在$\triangle ABD$和$\triangle CAE$中：
$\begin{cases}\angle BDA=\angle AEC\\\angle DBA=\angle CAE\\AB = AC\end{cases}$
根据$AAS$，可得$\triangle ABD\cong\triangle CAE$。
所以$BD = AE$，$AD = CE$。
又因为$DE=AD + AE$，所以$DE=BD + CE$。
综上，（1）得证$DE = BD+CE$；（2）$DE$，$BD$，$CE$三条线段的数量关系为$DE = BD + CE$。

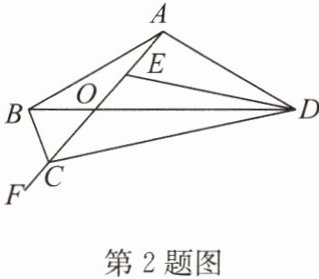
2.如图,在四边形ABCD中,$AB= AD$,AC与BD交于点O,点E,F在射线AC上,且$∠BCF= ∠DEF= ∠BAD$.若$OD= 4OB,△ABC$的面积为3,求$△CDE$的面积.

答案： 解:如答图,过点A作AG⊥BD于点G,过点C作CH⊥ BD于点H.
∵∠BCF=∠DEF=∠BAD,∠ACB+ ∠BCF=180°,∠DEF+∠AED=180°,
∴∠ACB= ∠AED.
∵∠BAC+∠DAE=∠BAD,∠ADE+ ∠DAE=∠DEF,
∴∠BAC=∠ADE.
又
∵AB=AD,
∴△ABC≌△DAE(AAS),
∴S△ABC=S△DAE=3.
∵OD= 4OB,
∴S△COD/S△COB=($\frac{1}{2}$ OD·CH)/($\frac{1}{2}$ OB·CH)=OD/OB=4OB/OB=4,S△AOD/S△AOB
= ($\frac{1}{2}$ OD·AG)/($\frac{1}{2}$ OB·AG)=OD/OB=4OB/OB=4,
∴S△COD=4S△COB, S△AOD=4S△AOB,
∴S△COD+S△AOD=4S△COB+4S△AOB= 4(S△COB+S△AOB)=4S△ABC=4×3=12.
∵S△COD+S△AOD=S△CDE+S△ADE=S△CDE+3,
∴S△CDE+3=12,
∴S△CDE=9.