《2025年启东中学作业本八年级数学上册苏科版盐城专版》

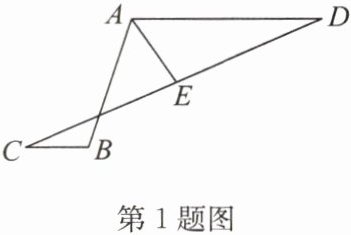
1. 如图,线段AD//BC,连接AB,CD,取CD的中点E,连接AE,AE恰好平分∠BAD.线段AB,AD,BC之间存在怎样的等量关系？并证明你的结论.

答案： 解：$AB = AD + BC$。
证明：延长$AE$、$BC$交于点$F$。
因为$AD// BC$，所以$\angle DAE=\angle F$（两直线平行，内错角相等）。
又因为$AE$平分$\angle BAD$，所以$\angle DAE = \angle BAE$，则$\angle BAE=\angle F$，所以$AB = BF$（等角对等边）。
因为$E$是$CD$中点，所以$DE = CE$。
在$\triangle ADE$和$\triangle FCE$中：
$\begin{cases}\angle DAE=\angle F\\\angle AED=\angle FEC\\DE = CE\end{cases}$
所以$\triangle ADE\cong\triangle FCE(AAS)$（角角边定理）。
所以$AD = CF$（全等三角形对应边相等）。
因为$BF=BC + CF$，$AD = CF$，$AB = BF$，所以$AB = AD + BC$。
综上，$AB$，$AD$，$BC$之间的等量关系为$AB = AD + BC$。

2. 如图,在四边形ABCD中,AB//CD,AB= 5,CD= 2.E为边BC的中点,连接AE,DE.若AE⊥DE,求AD的长.

答案： 解：延长$AE$交$DC$的延长线于点$F$。
因为$AB// CD$，所以$\angle B=\angle ECF$，$\angle BAE=\angle F$。
又因为$E$为$BC$的中点，即$BE = CE$，所以$\triangle ABE\cong\triangle FCE(AAS)$。
则$AE = FE$，$AB = FC = 5$。
因为$AE\perp DE$，所以$DE$是线段$AF$的垂直平分线，所以$AD = FD$。
已知$CD = 2$，$FC = 5$，所以$FD=FC + CD=5 + 2=7$，即$AD = 7$。
综上，$AD$的长为$7$。