《2025年启东中学作业本八年级数学上册苏科版盐城专版》

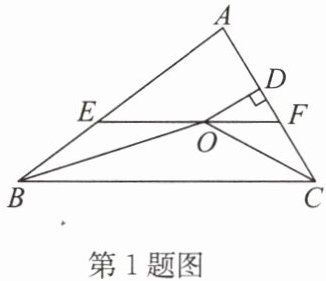
1. 如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点 O,过点 O 作 EF//BC 交 AB 于点 E,交 AC 于点 F,过点 O 作 OD⊥AC 于点 D。下列四个结论：①EF= BE+CF；②∠BOC= 90°+1/2∠A；③点 O 到△ABC 各边的距离相等；④设 OD= m,AE+AF= n,则 S_{△AEF}= 1/2mn。其中正确的结论有(D)

A.1 个
B.2 个
C.3 个
D.4 个

答案： D

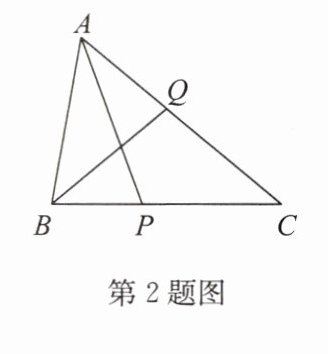
2. 如图,在△ABC 中,∠BAC= 60°,∠C= 40°,点 P,Q 分别在 BC,CA 上,AP,BQ 分别是∠BAC,∠ABC 的平分线。求证：BQ+AQ= AB+BP。

答案： 解：
在$AB$上截取$AD = AQ$，连接$PD$。
因为$AP$是$\angle BAC$的平分线，所以$\angle BAP=\angle CAP = \frac{1}{2}\angle BAC=\frac{1}{2}×60^{\circ}=30^{\circ}$。
在$\triangle AQD$和$\triangle APD$中：
$\begin{cases}AD = AQ\\\angle BAP=\angle CAP\\AP = AP\end{cases}$
根据$SAS$（边角边）定理可得$\triangle AQD\cong\triangle APD$。
所以$\angle ADP=\angle AQP$。
在$\triangle ABC$中，$\angle ABC=180^{\circ}-\angle BAC - \angle C=180^{\circ}-60^{\circ}-40^{\circ}=80^{\circ}$。
因为$BQ$是$\angle ABC$的平分线，所以$\angle QBC=\frac{1}{2}\angle ABC = 40^{\circ}$，则$\angle AQP=\angle QBC+\angle C=40^{\circ}+40^{\circ}=80^{\circ}$，所以$\angle ADP = 80^{\circ}$。
又因为$\angle BDP = 180^{\circ}-\angle ADP=100^{\circ}$，$\angle BPD=180^{\circ}-\angle B - \angle BAP=180^{\circ}-80^{\circ}-30^{\circ}=70^{\circ}$，$\angle C = 40^{\circ}$，$\angle APC=\angle B+\angle BAP=80^{\circ}+30^{\circ}=110^{\circ}$，$\angle DPB = 180^{\circ}-\angle APC+\angle C=180^{\circ}-110^{\circ}+40^{\circ}=70^{\circ}$，所以$\angle BDP = 180^{\circ}-\angle DBP-\angle DPB=180^{\circ}-40^{\circ}-70^{\circ}=70^{\circ}$，即$\angle DBP=\angle DPB$，所以$BD = BP$。
因为$AB=AD + BD$，$AD = AQ$，$BD = BP$，所以$AB+BP=AD + BD+BP=AQ + BQ$，即$BQ + AQ=AB + BP$。
综上，$BQ + AQ=AB + BP$得证。

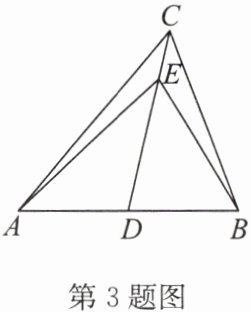
3. (1)如图,在△ABC 中,CD 是中线,点 E 在 CD 上,且 AE= BC,求证：∠AED= ∠BCD；
(2)在(1)的条件下,连接 BE,若 AB= 2DE,∠CBE= 10°,求∠BED 的度数。

答案：

(1)证明:如答图，延长CD到点F,使DF=CD,连接AF;
∵CD为△ABC的中线,
∴AD=BD.
∵∠ADF=∠BDC,DF=DC,
∴△ADF≌△BDC(SAS),
∴AF=BC,∠F=∠BCD.
∵AE=BC,
∴AE=AF,
∴∠AED=∠F,
∴∠AED=∠BCD.
　　　　　　　　　
(2)解:
∵CD为△ABC的中线,
∴AD=BD=$\frac{1}{2}$AB.
∵AB=2DE,
∴AD=BD=ED,
∴∠AED=∠EAD,∠BED=∠EBD.
∵∠AED+∠EAD+∠BED+∠EBD=180°,
∴∠AED+∠BED=90°,由
(1)知∠AED=∠BCD,
∴∠BCD+∠BED=90°.
∵∠BED=∠BCD+∠EBC=∠BCD+10°,
∴∠BCD+∠BCD+10°=90°,
∴∠BCD=40°,
∴∠BED=50°.