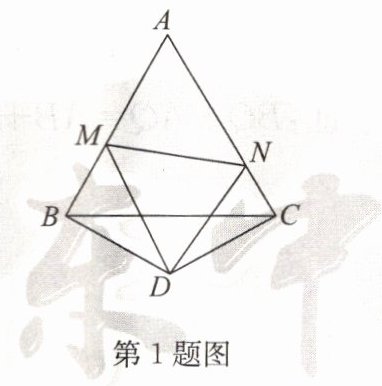
1. 如图,$△ABC$是边长为 4 的等边三角形,$BD= CD$,且$∠BDC= 120^{\circ }$,以 D 为顶点作一个$60^{\circ }$角,使其两边分别交 AB 于点 M,交 AC 于点 N,连接 MN,则$△AMN$的周长是____.

答案:
8 点拨:如答图,延长AB至点F,使BF=CN,连接DF.
∵△BDC是等腰三角形,且∠BDC=120°,
∴∠BCD=∠DBC=30°.
∵△ABC是边长为4的等边三角形,
∴∠ABC=∠BAC=∠BCA=60°,
∴∠DBA=∠DCA=∠FBD=90°.
在△BDF和△CDN中,{BF=CN,∠DBF=∠DCN,DB=DC}
∴△BDF≌△CDN(SAS),
∴∠BDF=∠CDN,DF=DN.
∵∠BDC=120°,∠MDN=60°,
∴∠BDM+∠CDN=60°,
∴∠MDF=∠BDM+∠BDF=60°,
∴∠MDN=∠MDF.
在△DMN和△DMF中,{MD=MD,∠MDN=∠MDF,DN=DF}
∴△DMN≌△DMF(SAS),
∴MN=MF,
∴△AMN的周长是AM+AN+MN=AM+MB+BF+AN=AB+AC=4+4=8.

8 点拨:如答图,延长AB至点F,使BF=CN,连接DF.
∵△BDC是等腰三角形,且∠BDC=120°,
∴∠BCD=∠DBC=30°.
∵△ABC是边长为4的等边三角形,
∴∠ABC=∠BAC=∠BCA=60°,
∴∠DBA=∠DCA=∠FBD=90°.
在△BDF和△CDN中,{BF=CN,∠DBF=∠DCN,DB=DC}
∴△BDF≌△CDN(SAS),
∴∠BDF=∠CDN,DF=DN.
∵∠BDC=120°,∠MDN=60°,
∴∠BDM+∠CDN=60°,
∴∠MDF=∠BDM+∠BDF=60°,
∴∠MDN=∠MDF.
在△DMN和△DMF中,{MD=MD,∠MDN=∠MDF,DN=DF}
∴△DMN≌△DMF(SAS),
∴MN=MF,
∴△AMN的周长是AM+AN+MN=AM+MB+BF+AN=AB+AC=4+4=8.

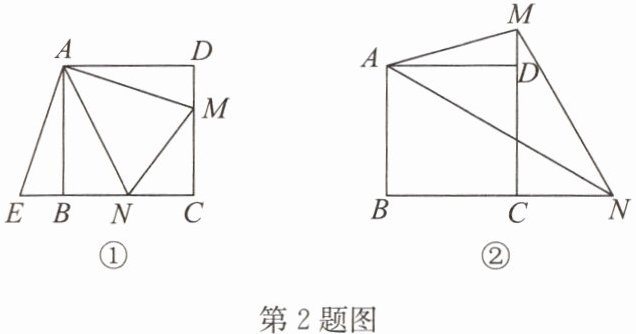
2. 如图①,四边形 ABCD 是正方形,点 M,N 分别在边 CD,BC 上,且$∠MAN= 45^{\circ }$,我们把这种模型称为“半角模型”. 在解决“半角模型”问题时,旋转是一种常用的方法,如图①,将$△ADM$绕点 A 顺时针旋转$90^{\circ }$,点 D 与点 B 重合,得到$△ABE$.
(1)试判断 DM,BN,MN 之间的数量关系,并写出证明过程;
(2)如图①,如果正方形的边长为 4,求$△CMN$的周长;
(3)如图②,点 M,N 分别在正方形 ABCD 的边 CD,BC 的延长线上,$∠MAN= 45^{\circ }$,连接 MN,请写出 MN,DM,BN 之间的数量关系,并写出证明过程.
(1)试判断 DM,BN,MN 之间的数量关系,并写出证明过程;
(2)如图①,如果正方形的边长为 4,求$△CMN$的周长;
(3)如图②,点 M,N 分别在正方形 ABCD 的边 CD,BC 的延长线上,$∠MAN= 45^{\circ }$,连接 MN,请写出 MN,DM,BN 之间的数量关系,并写出证明过程.

答案:
1. (1)
判断数量关系并证明**:
数量关系:$MN = BN + DM$。
证明:
由旋转可知$\triangle ADM\cong\triangle ABE$,所以$AM = AE$,$DM = BE$,$\angle DAM=\angle BAE$。
因为四边形$ABCD$是正方形,所以$\angle DAB = 90^{\circ}$,又$\angle MAN = 45^{\circ}$,则$\angle BAN+\angle DAM = 45^{\circ}$。
所以$\angle BAN+\angle BAE=\angle EAN = 45^{\circ}$,即$\angle EAN=\angle MAN$。
在$\triangle AEN$和$\triangle AMN$中,$\left\{\begin{array}{l}AE = AM\\\angle EAN=\angle MAN\\AN = AN\end{array}\right.$。
根据$SAS$(边角边)定理可得$\triangle AEN\cong\triangle AMN$。
所以$MN = EN$,又因为$EN = BE + BN$,$BE = DM$,所以$MN = BN + DM$。
2. (2)
求$\triangle CMN$的周长**:
因为$\triangle CMN$的周长$C = CM + CN+MN$。
由(1)知$MN = BN + DM$,所以$C = CM + CN+(BN + DM)$。
又因为$CM + DM = CD$,$CN + BN = BC$,正方形边长$CD = BC = 4$。
所以$C = CD + BC=4 + 4=8$。
3. (3)
判断数量关系并证明**:
数量关系:$MN = BN - DM$。
证明:
将$\triangle ADM$绕点$A$顺时针旋转$90^{\circ}$,点$D$与点$B$重合,得到$\triangle ABF$。
则$AM = AF$,$DM = BF$,$\angle DAM=\angle BAF$。
因为$\angle MAN = 45^{\circ}$,$\angle DAB = 90^{\circ}$,所以$\angle BAN-\angle DAM = 45^{\circ}$。
即$\angle NAF=\angle BAN-\angle BAF = 45^{\circ}$,所以$\angle NAF=\angle MAN$。
在$\triangle AMN$和$\triangle AFN$中,$\left\{\begin{array}{l}AM = AF\\\angle MAN=\angle FAN\\AN = AN\end{array}\right.$。
根据$SAS$定理可得$\triangle AMN\cong\triangle AFN$。
所以$MN = FN$,又因为$FN = BN - BF$,$BF = DM$,所以$MN = BN - DM$。
综上,(1)$MN = BN + DM$;(2)$8$;(3)$MN = BN - DM$。
判断数量关系并证明**:
数量关系:$MN = BN + DM$。
证明:
由旋转可知$\triangle ADM\cong\triangle ABE$,所以$AM = AE$,$DM = BE$,$\angle DAM=\angle BAE$。
因为四边形$ABCD$是正方形,所以$\angle DAB = 90^{\circ}$,又$\angle MAN = 45^{\circ}$,则$\angle BAN+\angle DAM = 45^{\circ}$。
所以$\angle BAN+\angle BAE=\angle EAN = 45^{\circ}$,即$\angle EAN=\angle MAN$。
在$\triangle AEN$和$\triangle AMN$中,$\left\{\begin{array}{l}AE = AM\\\angle EAN=\angle MAN\\AN = AN\end{array}\right.$。
根据$SAS$(边角边)定理可得$\triangle AEN\cong\triangle AMN$。
所以$MN = EN$,又因为$EN = BE + BN$,$BE = DM$,所以$MN = BN + DM$。
2. (2)
求$\triangle CMN$的周长**:
因为$\triangle CMN$的周长$C = CM + CN+MN$。
由(1)知$MN = BN + DM$,所以$C = CM + CN+(BN + DM)$。
又因为$CM + DM = CD$,$CN + BN = BC$,正方形边长$CD = BC = 4$。
所以$C = CD + BC=4 + 4=8$。
3. (3)
判断数量关系并证明**:
数量关系:$MN = BN - DM$。
证明:
将$\triangle ADM$绕点$A$顺时针旋转$90^{\circ}$,点$D$与点$B$重合,得到$\triangle ABF$。
则$AM = AF$,$DM = BF$,$\angle DAM=\angle BAF$。
因为$\angle MAN = 45^{\circ}$,$\angle DAB = 90^{\circ}$,所以$\angle BAN-\angle DAM = 45^{\circ}$。
即$\angle NAF=\angle BAN-\angle BAF = 45^{\circ}$,所以$\angle NAF=\angle MAN$。
在$\triangle AMN$和$\triangle AFN$中,$\left\{\begin{array}{l}AM = AF\\\angle MAN=\angle FAN\\AN = AN\end{array}\right.$。
根据$SAS$定理可得$\triangle AMN\cong\triangle AFN$。
所以$MN = FN$,又因为$FN = BN - BF$,$BF = DM$,所以$MN = BN - DM$。
综上,(1)$MN = BN + DM$;(2)$8$;(3)$MN = BN - DM$。
查看更多完整答案,请扫码查看


