1. 如图, 在平面直角坐标系中, 直线 AB 分别交 x 轴, y 轴于点 $ A(a,0),B(0,b) $, 且满足 $ \sqrt { a + 3 } + ( b - 6 ) ^ { 2 } = 0 $.
(1) 求 a,b 的值和 $ \triangle AOB $ 的面积;
(2) 在 x 轴的正半轴上取一点 P, 使得 $ S _ { \triangle P O B } = 3 S _ { \triangle A O B } $, 求 OP 的长;
(3) 若点 P 在直线 AB 的右侧, 且 $ \triangle ABP $ 为等腰直角三角形, 求点 P 的坐标.
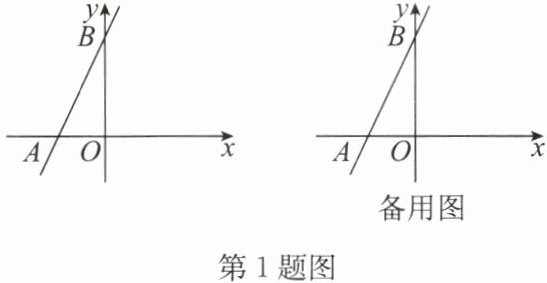
(1) 求 a,b 的值和 $ \triangle AOB $ 的面积;
(2) 在 x 轴的正半轴上取一点 P, 使得 $ S _ { \triangle P O B } = 3 S _ { \triangle A O B } $, 求 OP 的长;
(3) 若点 P 在直线 AB 的右侧, 且 $ \triangle ABP $ 为等腰直角三角形, 求点 P 的坐标.

答案:
1.解:
(1)
∵$\sqrt{a+3}$+(b−6)²=0,
∴$\sqrt{a+3}$=0,(b−6)²=0,
∴a=−3,b=6,
∴A(−3,0),B(0,6),
∴OA=3,OB=6,
∴S△AOB=$\frac{1}{2}$OA·OB=9.
(2)
∵S△POB=3S△AOB,
∴S△POB=$\frac{1}{2}$OP·OB=27.
∵OB=6,
∴OP=9.
(3)①如答图①,若△ABP是以∠ABP为直角的等腰直角三角形,则∠BAP=∠APB=45°.过点P作PC⊥OB,垂足为C,

∴∠PCB=∠BOA=90°.
又
∵∠ABO+∠OBP=∠OBP+∠BPC=90°,
∴∠ABO=∠BPC,又AB=BP,
∴△ABO≌△BPC(AAS),
∴PC=OB=6,BC=OA=3,
∴OC=OB−BC=6−3=3,
∴P(6,3).
②如答图②,若△ABP是以∠BAP为直角的等腰直角三角形,则AB=AP,∠ABP=∠APB=45°,过点P作PD⊥OA,垂足为D,

易证△BAO≌△APD,
∴PD=OA=3,AD=OB=6,
∴OD=AD−OA=6−3=3,
∴P(3,−3).
③如答图③,若△ABP是以∠APB为直角的等腰直角三角形,则AP=PB,∠BAP=∠ABP=45°,过点P作PD⊥OA于点D,PC⊥OB于点C,

易证△BCP≌△ADP,
∴AD=BC,PC=PD=CO=OD,设AD=x,PC=y,则$\begin{cases}x + y = 6\\x - y = 3\end{cases}$,解得$\begin{cases}x = \frac{9}{2}\\y = \frac{3}{2}\end{cases}$,
∴P($\frac{3}{2}$,$\frac{3}{2}$).
综上所述,点P的坐标为(6,3)或(3,−3)或($\frac{3}{2}$,$\frac{3}{2}$).
1.解:
(1)
∵$\sqrt{a+3}$+(b−6)²=0,
∴$\sqrt{a+3}$=0,(b−6)²=0,
∴a=−3,b=6,
∴A(−3,0),B(0,6),
∴OA=3,OB=6,
∴S△AOB=$\frac{1}{2}$OA·OB=9.
(2)
∵S△POB=3S△AOB,
∴S△POB=$\frac{1}{2}$OP·OB=27.
∵OB=6,
∴OP=9.
(3)①如答图①,若△ABP是以∠ABP为直角的等腰直角三角形,则∠BAP=∠APB=45°.过点P作PC⊥OB,垂足为C,

∴∠PCB=∠BOA=90°.
又
∵∠ABO+∠OBP=∠OBP+∠BPC=90°,
∴∠ABO=∠BPC,又AB=BP,
∴△ABO≌△BPC(AAS),
∴PC=OB=6,BC=OA=3,
∴OC=OB−BC=6−3=3,
∴P(6,3).
②如答图②,若△ABP是以∠BAP为直角的等腰直角三角形,则AB=AP,∠ABP=∠APB=45°,过点P作PD⊥OA,垂足为D,

易证△BAO≌△APD,
∴PD=OA=3,AD=OB=6,
∴OD=AD−OA=6−3=3,
∴P(3,−3).
③如答图③,若△ABP是以∠APB为直角的等腰直角三角形,则AP=PB,∠BAP=∠ABP=45°,过点P作PD⊥OA于点D,PC⊥OB于点C,

易证△BCP≌△ADP,
∴AD=BC,PC=PD=CO=OD,设AD=x,PC=y,则$\begin{cases}x + y = 6\\x - y = 3\end{cases}$,解得$\begin{cases}x = \frac{9}{2}\\y = \frac{3}{2}\end{cases}$,
∴P($\frac{3}{2}$,$\frac{3}{2}$).
综上所述,点P的坐标为(6,3)或(3,−3)或($\frac{3}{2}$,$\frac{3}{2}$).
2. 如图①, 在平面直角坐标系中, 直线 $ A B : y = - \frac { 3 } { 4 } x + b $ 交 x 轴于点 $ A ( 8,0 ) $, 交 y 轴正半轴于点 B.
(1) 求点 B 的坐标;
(2) 如图②, 直线 AC 交 y 轴负半轴于点 C, $ A B = B C $, P 为线段 AB 上一点, 过点 P 作 y 轴的平行线交直线 AC 于点 Q, 设点 P 的横坐标为 t, 线段 PQ 的长为 d, 求 d 与 t 之间的函数表达式;
(3) 在 (2) 的条件下, M 为 CA 延长线上一点, 且 $ A M = C Q $, 在直线 AC 上方的直线 AB 上是否存在点 N, 使 $ \triangle Q M N $ 是以 QM 为斜边的等腰直角三角形? 若存在, 请求出点 N 的坐标及 PN 的长度; 若不存在, 请说明理由.
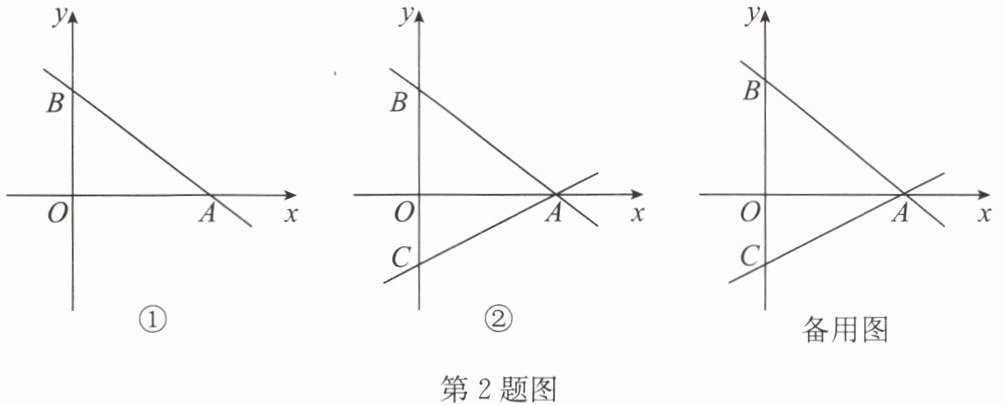
(1) 求点 B 的坐标;
(2) 如图②, 直线 AC 交 y 轴负半轴于点 C, $ A B = B C $, P 为线段 AB 上一点, 过点 P 作 y 轴的平行线交直线 AC 于点 Q, 设点 P 的横坐标为 t, 线段 PQ 的长为 d, 求 d 与 t 之间的函数表达式;
(3) 在 (2) 的条件下, M 为 CA 延长线上一点, 且 $ A M = C Q $, 在直线 AC 上方的直线 AB 上是否存在点 N, 使 $ \triangle Q M N $ 是以 QM 为斜边的等腰直角三角形? 若存在, 请求出点 N 的坐标及 PN 的长度; 若不存在, 请说明理由.

答案:
2.解:
(1)
∵直线y=−$\frac{3}{4}$x+b交x轴于点A(8,0),
∴0=−$\frac{3}{4}$×8+b,
∴b=6,
∴直线AB的函数表达式为y=−$\frac{3}{4}$x+6,
令x=0,则y=6,
∴B(0,6).
(2)
∵A(8,0),B(0,6),
∴OA=8,OB=6.
∵∠AOB=90°,
∴AB=$\sqrt{OA^{2}+OB^{2}}$=10=BC,
∴OC=4,
∴C(0,−4).
设直线AC的函数表达式为y=kx+b',
∴$\begin{cases}0 = 8k + b'\\-4 = b'\end{cases}$,解得$\begin{cases}k = \frac{1}{2}\\b' = -4\end{cases}$,
∴直线AC的函数表达式为y=$\frac{1}{2}$x−4.
∵点P在直线y=−$\frac{3}{4}$x+6上,
∴设点P(t,−$\frac{3}{4}$t+6).
∵PQ//y轴,且点Q在直线y=$\frac{1}{2}$x−4上,
∴Q(t,$\frac{1}{2}$t−4),
∴d=(−$\frac{3}{4}$t+6)−($\frac{1}{2}$t−4)=−$\frac{5}{4}$t+10.
(3)存在.如答图,过点M作MG⊥PQ于点G,
∴∠QGM=90°=∠COA.
∵PQ//y轴,
∴∠OCA=∠GQM.
∵CQ=AM,
∴AC=QM.
在△OAC与△GMQ中,$\begin{cases}∠AOC = ∠MGQ\\∠ACO = ∠MQG\\AC = MQ\end{cases}$,
∴△OAC≌△GMQ,
∴QG=OC=4,GM=OA=8.
过点N作NH⊥PQ于点H,过点M作MR⊥NH于点R,
∴∠MGH=∠RHG=∠MRH=90°,
∴四边形GHRM是长方形,
∴HR=GM=8.设GH=RM=m,
∵△MNQ是等腰直角三角形,
∴∠QNM=90°,NQ=NM,
∴∠HNQ+∠HQN=90°,∠HNQ+∠RNM=90°,
∴∠RNM=∠HQN,
∴△HNQ≌△RMN,
∴HN=RM=m,NR=QH=4+m.
∵HR=HN+NR,
∴m+4+m=8,
∴m=2,
∴GH=NH=RM=2,
∴HQ=6.
∵Q(t,$\frac{1}{2}$t−4),
∴N(t+2,$\frac{1}{2}$t−4+6),即N(t+2,$\frac{1}{2}$t+2).
∵点N在直线AB:y=−$\frac{3}{4}$x+6上,
∴$\frac{1}{2}$t+2=−$\frac{3}{4}$(t+2)+6,解得t=2,
∴P(2,$\frac{9}{2}$),N(4,3),
∴PH=$\frac{3}{2}$,
∴PN=$\sqrt{PH^{2}+NH^{2}}$=$\frac{5}{2}$.

2.解:
(1)
∵直线y=−$\frac{3}{4}$x+b交x轴于点A(8,0),
∴0=−$\frac{3}{4}$×8+b,
∴b=6,
∴直线AB的函数表达式为y=−$\frac{3}{4}$x+6,
令x=0,则y=6,
∴B(0,6).
(2)
∵A(8,0),B(0,6),
∴OA=8,OB=6.
∵∠AOB=90°,
∴AB=$\sqrt{OA^{2}+OB^{2}}$=10=BC,
∴OC=4,
∴C(0,−4).
设直线AC的函数表达式为y=kx+b',
∴$\begin{cases}0 = 8k + b'\\-4 = b'\end{cases}$,解得$\begin{cases}k = \frac{1}{2}\\b' = -4\end{cases}$,
∴直线AC的函数表达式为y=$\frac{1}{2}$x−4.
∵点P在直线y=−$\frac{3}{4}$x+6上,
∴设点P(t,−$\frac{3}{4}$t+6).
∵PQ//y轴,且点Q在直线y=$\frac{1}{2}$x−4上,
∴Q(t,$\frac{1}{2}$t−4),
∴d=(−$\frac{3}{4}$t+6)−($\frac{1}{2}$t−4)=−$\frac{5}{4}$t+10.
(3)存在.如答图,过点M作MG⊥PQ于点G,
∴∠QGM=90°=∠COA.
∵PQ//y轴,
∴∠OCA=∠GQM.
∵CQ=AM,
∴AC=QM.
在△OAC与△GMQ中,$\begin{cases}∠AOC = ∠MGQ\\∠ACO = ∠MQG\\AC = MQ\end{cases}$,
∴△OAC≌△GMQ,
∴QG=OC=4,GM=OA=8.
过点N作NH⊥PQ于点H,过点M作MR⊥NH于点R,
∴∠MGH=∠RHG=∠MRH=90°,
∴四边形GHRM是长方形,
∴HR=GM=8.设GH=RM=m,
∵△MNQ是等腰直角三角形,
∴∠QNM=90°,NQ=NM,
∴∠HNQ+∠HQN=90°,∠HNQ+∠RNM=90°,
∴∠RNM=∠HQN,
∴△HNQ≌△RMN,
∴HN=RM=m,NR=QH=4+m.
∵HR=HN+NR,
∴m+4+m=8,
∴m=2,
∴GH=NH=RM=2,
∴HQ=6.
∵Q(t,$\frac{1}{2}$t−4),
∴N(t+2,$\frac{1}{2}$t−4+6),即N(t+2,$\frac{1}{2}$t+2).
∵点N在直线AB:y=−$\frac{3}{4}$x+6上,
∴$\frac{1}{2}$t+2=−$\frac{3}{4}$(t+2)+6,解得t=2,
∴P(2,$\frac{9}{2}$),N(4,3),
∴PH=$\frac{3}{2}$,
∴PN=$\sqrt{PH^{2}+NH^{2}}$=$\frac{5}{2}$.

查看更多完整答案,请扫码查看


