《2025年启东中学作业本八年级数学上册苏科版盐城专版》

1. 如图,在四边形ABDC中,对角线AD平分∠BAC,∠ACD= 136°,∠BCD= 44°,则∠ADB的度数为(D)
A.54°
B.50°
C.48°
D.46°

答案： 1.D

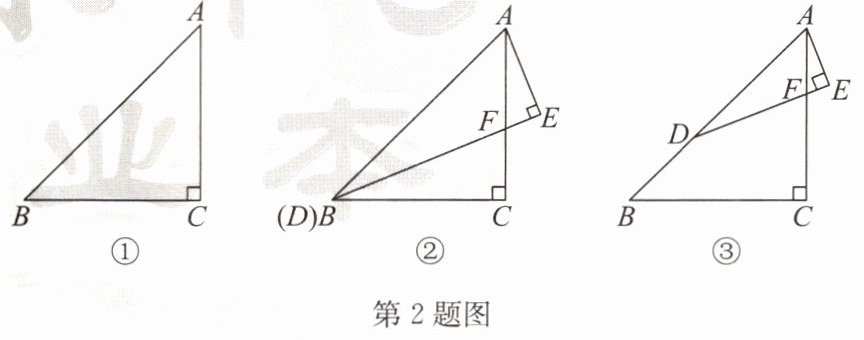
2. 在Rt△ABC中,∠ACB= 90°,∠ABC= 45°,D为边AB上一点,DE⊥AE于点E,AC与DE交于点F,∠ADE= 22.5°。
(1)如图①,求证：AC= BC；
(2)如图②,当点D与点B重合时,求证：BF= 2AE；
(3)如图③,若点D不与点A,B重合,AE= 3,求△ADF的面积。

答案： 1. （1）证明：
在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$\angle ABC=45^{\circ}$。
根据三角形内角和定理$\angle A+\angle ABC+\angle ACB = 180^{\circ}$，则$\angle A=180^{\circ}-\angle ACB - \angle ABC$。
把$\angle ACB = 90^{\circ}$，$\angle ABC = 45^{\circ}$代入得$\angle A=180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ}$。
所以$\angle A=\angle ABC$，根据等角对等边，可得$AC = BC$。
2. （2）证明：
延长$AE$交$CB$的延长线于点$G$。
因为$BE\perp AE$，所以$\angle BEA=\angle BEG = 90^{\circ}$。
又因为$\angle ADE=\angle CBE = 22.5^{\circ}$，$\angle ABC = 45^{\circ}$，所以$\angle ABG = 180^{\circ}-\angle ABC=135^{\circ}$，$\angle AB E=\angle ABC+\angle CBE=45^{\circ}+22.5^{\circ}=67.5^{\circ}$，$\angle G=\angle ABG-\angle BAG$，$\angle BAG = 45^{\circ}-22.5^{\circ}=22.5^{\circ}$，$\angle G = 180^{\circ}-\angle AB E-\angle BAE=90^{\circ}-\angle BAE$。
在$\triangle BAE$和$\triangle BGE$中，$\left\{\begin{array}{l}\angle BEA=\angle BEG\\ BE = BE\\ \angle ABE=\angle GBE\end{array}\right.$（$\angle GBE=\angle ABC + \angle CBE$，$\angle ABE=\angle ABC+\angle CBE$，因为$BE$平分$\angle ABG$，$\angle ABG = 135^{\circ}$，$\angle ABE=\angle GBE = 67.5^{\circ}$）。
根据$ASA$（角 - 边 - 角）定理，$\triangle BAE\cong\triangle BGE$，所以$AE = GE$，即$AG = 2AE$。
因为$\angle ACB=\angle BEG = 90^{\circ}$，所以$AC// BG$，则$\angle FAC=\angle G$。
在$\triangle ACF$和$\triangle BCG$中，$\left\{\begin{array}{l}\angle FAC=\angle G\\\angle ACF=\angle BCG = 90^{\circ}\\AC = BC\end{array}\right.$。
根据$AAS$（角 - 角 - 边）定理，$\triangle ACF\cong\triangle BCG$，所以$AF = BG$。
又因为$\angle ABG = 135^{\circ}$，$\angle BAG = 22.5^{\circ}$，$\angle AFB=\angle BAG+\angle ABF$（外角定理），$\angle ABF = 45^{\circ}$，$\angle BAG = 22.5^{\circ}$，$\angle AFB = 67.5^{\circ}$，$\angle ABG = 135^{\circ}$，$\angle G = 67.5^{\circ}$，$\angle AFB=\angle G$，$AF = BG$，$\angle FAC=\angle G$，$\angle ACF=\angle BCG$，$AC = BC$，$\triangle ACF\cong\triangle BCG$，所以$AF = BG$，$\angle FAB=\angle ABF = 22.5^{\circ}$，所以$BF = AF$，又$AG = 2AE$，$AF = AG$，所以$BF = 2AE$。
3. （3）解：
过点$D$作$DH\perp AC$于点$H$。
因为$\angle A = 45^{\circ}$，$\angle ADE = 22.5^{\circ}$，$\angle AFD=\angle ADE+\angle A$（外角定理），所以$\angle AFD = 22.5^{\circ}+45^{\circ}=67.5^{\circ}$。
又因为$\angle A = 45^{\circ}$，$\angle AED = 90^{\circ}$，$\angle ADE = 22.5^{\circ}$，$\angle FDH = 45^{\circ}-22.5^{\circ}=22.5^{\circ}$，$\angle DFH = 180^{\circ}-\angle AFD=112.5^{\circ}$，$\angle DAH = 45^{\circ}$，$\triangle ADH$是等腰直角三角形，$AH = DH$。
因为$\angle AED=\angle DHF = 90^{\circ}$，$\angle ADE=\angle HDF = 22.5^{\circ}$。
设$DH = AH=x$。
因为$\angle A = 45^{\circ}$，$\angle AED = 90^{\circ}$，所以$\angle ADE+\angle AFD = 90^{\circ}$，$\angle A = 45^{\circ}$，$\angle AED = 90^{\circ}$，$\triangle ADE$中，$\tan\angle A=\frac{DE}{AE}$，$\angle A = 45^{\circ}$，$AE = 3$，$DE = 3$。
又因为$\triangle DHF\sim\triangle AED$（$\angle AED=\angle DHF$，$\angle ADE=\angle HDF$），$\frac{AE}{DH}=\frac{DE}{FH}$。
因为$\angle A = 45^{\circ}$，$\angle AHD = 90^{\circ}$，$AH = DH$，$\angle ADE = 22.5^{\circ}$，$\angle FDH = 22.5^{\circ}$，$\triangle AED\cong\triangle DHF(AAS)$（$\angle AED=\angle DHF$，$\angle ADE=\angle HDF$，$AD = DA$），$FH = AE = 3$，$AH = DH = 3$。
$S_{\triangle ADF}=\frac{1}{2}AF\cdot DH$，$AF=AH + FH$，$AH = FH = 3$，$AF = 6$，$DH = 3$。
所以$S_{\triangle ADF}=\frac{1}{2}×6×3 = 9$。
综上，（1）得证$AC = BC$；（2）得证$BF = 2AE$；（3）$\triangle ADF$的面积为$9$。

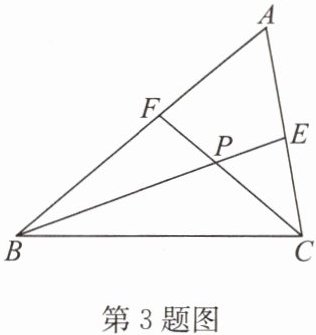
3. 如图,在△ABC中,∠A= 60°,BE,CF分别平分∠ABC,∠ACB,且交于点P。
(1)求∠BPC的度数；
(2)求证：FP= EP。

答案： 1. （1）
解：
在$\triangle ABC$中，根据三角形内角和定理$\angle A+\angle ABC+\angle ACB = 180^{\circ}$，已知$\angle A = 60^{\circ}$，则$\angle ABC+\angle ACB=180^{\circ}-\angle A=180 - 60=120^{\circ}$。
因为$BE$平分$\angle ABC$，$CF$平分$\angle ACB$，所以$\angle PBC=\frac{1}{2}\angle ABC$，$\angle PCB=\frac{1}{2}\angle ACB$。
那么$\angle PBC+\angle PCB=\frac{1}{2}(\angle ABC + \angle ACB)$。
把$\angle ABC+\angle ACB = 120^{\circ}$代入可得$\angle PBC+\angle PCB=\frac{1}{2}×120^{\circ}=60^{\circ}$。
在$\triangle BPC$中，根据三角形内角和定理$\angle BPC+\angle PBC+\angle PCB = 180^{\circ}$，所以$\angle BPC=180^{\circ}-(\angle PBC+\angle PCB)=180 - 60=120^{\circ}$。
2. （2）
证明：
在$BC$上截取$BD = BF$。
因为$BE$平分$\angle ABC$，所以$\angle FBP=\angle DBP$。
在$\triangle FBP$和$\triangle DBP$中，$\left\{\begin{array}{l}BF = BD\\\angle FBP=\angle DBP\\BP = BP\end{array}\right.$（$SAS$判定定理）。
所以$\triangle FBP\cong\triangle DBP$，则$\angle BPF=\angle BPD$，$FP = DP$。
因为$\angle BPC = 120^{\circ}$，所以$\angle BPF=\angle BPD = 60^{\circ}$，那么$\angle DPC=\angle BPC-\angle BPD=120 - 60 = 60^{\circ}$。
又因为$\angle EPC=180^{\circ}-\angle BPC=60^{\circ}$（邻补角定义），所以$\angle EPC=\angle DPC$。
因为$CF$平分$\angle ACB$，所以$\angle ECP=\angle DCP$。
在$\triangle EPC$和$\triangle DPC$中，$\left\{\begin{array}{l}\angle EPC=\angle DPC\\\angle ECP=\angle DCP\\PC = PC\end{array}\right.$（$ASA$判定定理）。
所以$\triangle EPC\cong\triangle DPC$，则$EP = DP$。
又因为$FP = DP$，所以$FP = EP$。
综上，（1）$\angle BPC$的度数为$120^{\circ}$；（2）证明过程如上述。