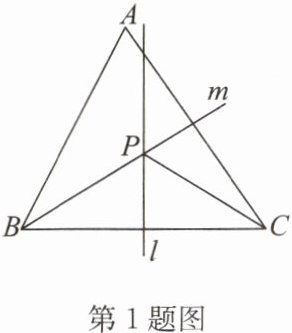
1. 如图,在锐角三角形ABC中,直线l为BC的垂直平分线,射线m为∠ABC的平分线,l与m相交于点P。若∠A= 60°,∠ACP= 24°,则∠ABP的度数为 (
A.24°
B.30°
C.32°
D.36°
C
)
A.24°
B.30°
C.32°
D.36°
答案:
C
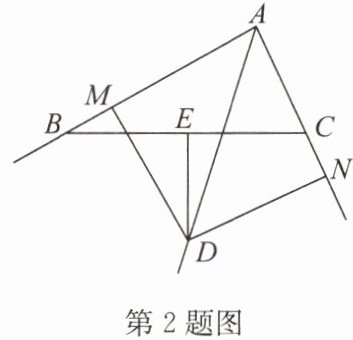
2. 如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC,交AC的延长线于点N。
(1)求证:BM= CN;
(2)若AB= 8,AC= 4,求BM的长。
(1)求证:BM= CN;
(2)若AB= 8,AC= 4,求BM的长。

答案:
1. (1)证明:
连接$BD$,$CD$。
因为$AD$平分$\angle CAB$,$DM\perp AB$,$DN\perp AC$,根据角平分线的性质定理:角平分线上的点到角两边的距离相等,所以$DM = DN$。
又因为$DE$是$BC$的垂直平分线,根据线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等,所以$BD = CD$。
在$Rt\triangle BMD$和$Rt\triangle CND$中,$\left\{\begin{array}{l}BD = CD\\DM = DN\end{array}\right.$。
根据$HL$(斜边 - 直角边)定理:如果两个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等,可得$Rt\triangle BMD\cong Rt\triangle CND$。
所以$BM = CN$。
2. (2)解:
因为$AD$平分$\angle CAB$,$DM\perp AB$,$DN\perp AC$,所以$\angle AMD=\angle AND = 90^{\circ}$,$\angle MAD=\angle NAD$,又$AD = AD$。
根据$AAS$(角 - 角 - 边)定理:如果两个三角形的两个角和其中一个角的对边分别相等,那么这两个三角形全等,可得$\triangle AMD\cong\triangle AND$,所以$AM = AN$。
因为$AM=AB - BM$,$AN=AC + CN$,又$BM = CN$。
设$BM=x$,则$AM = 8 - x$,$AN=4 + x$。
所以$8 - x=4 + x$。
移项可得:$-x - x=4 - 8$,即$-2x=-4$。
两边同时除以$-2$:$x = 2$。
所以(1)已证$BM = CN$;(2)$BM$的长为$2$。
连接$BD$,$CD$。
因为$AD$平分$\angle CAB$,$DM\perp AB$,$DN\perp AC$,根据角平分线的性质定理:角平分线上的点到角两边的距离相等,所以$DM = DN$。
又因为$DE$是$BC$的垂直平分线,根据线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等,所以$BD = CD$。
在$Rt\triangle BMD$和$Rt\triangle CND$中,$\left\{\begin{array}{l}BD = CD\\DM = DN\end{array}\right.$。
根据$HL$(斜边 - 直角边)定理:如果两个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等,可得$Rt\triangle BMD\cong Rt\triangle CND$。
所以$BM = CN$。
2. (2)解:
因为$AD$平分$\angle CAB$,$DM\perp AB$,$DN\perp AC$,所以$\angle AMD=\angle AND = 90^{\circ}$,$\angle MAD=\angle NAD$,又$AD = AD$。
根据$AAS$(角 - 角 - 边)定理:如果两个三角形的两个角和其中一个角的对边分别相等,那么这两个三角形全等,可得$\triangle AMD\cong\triangle AND$,所以$AM = AN$。
因为$AM=AB - BM$,$AN=AC + CN$,又$BM = CN$。
设$BM=x$,则$AM = 8 - x$,$AN=4 + x$。
所以$8 - x=4 + x$。
移项可得:$-x - x=4 - 8$,即$-2x=-4$。
两边同时除以$-2$:$x = 2$。
所以(1)已证$BM = CN$;(2)$BM$的长为$2$。
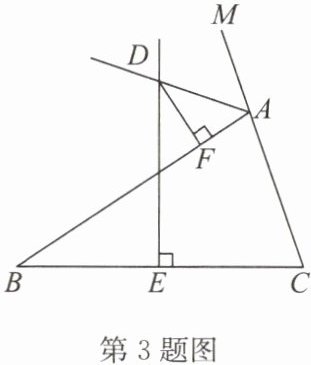
3. 如图,△ABC的边BC的垂直平分线DE交△ABC的外角平分线AD于点D,DF⊥AB于点F,且AB>AC,试探究BF,AC,AF之间的数量关系,并说明理由。

答案:
1. 首先,过点$D$作$DG\perp AC$,交$CA$的延长线于点$G$:
因为$AD$是$\triangle ABC$的外角平分线,$DF\perp AB$,$DG\perp AC$,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$DF = DG$。
又因为$DE$是$BC$的垂直平分线,根据垂直平分线的性质:线段垂直平分线上的点到线段两端的距离相等,所以$DB = DC$。
2. 然后,证明$Rt\triangle DFB\cong Rt\triangle DGC$:
在$Rt\triangle DFB$和$Rt\triangle DGC$中,$\left\{\begin{array}{l}DB = DC\\DF = DG\end{array}\right.$($HL$定理:斜边和一条直角边对应相等的两个直角三角形全等)。
所以$BF = CG$。
3. 接着,证明$Rt\triangle DFA\cong Rt\triangle DGA$:
在$Rt\triangle DFA$和$Rt\triangle DGA$中,$\left\{\begin{array}{l}AD = AD\\DF = DG\end{array}\right.$($HL$定理)。
所以$AF = AG$。
4. 最后,探究$BF$,$AC$,$AF$之间的数量关系:
因为$CG=AC + AG$,又$BF = CG$,$AF = AG$。
解:$BF=AC + AF$。
理由:过点$D$作$DG\perp AC$,交$CA$的延长线于点$G$。
由于$AD$平分$\angle BAG$(外角),$DF\perp AB$,$DG\perp AC$,根据角平分线性质$DF = DG$;又$DE$垂直平分$BC$,所以$DB = DC$。
在$Rt\triangle DFB$和$Rt\triangle DGC$中,$\left\{\begin{array}{l}DB = DC\\DF = DG\end{array}\right.$,由$HL$定理得$Rt\triangle DFB\cong Rt\triangle DGC$,则$BF = CG$。
在$Rt\triangle DFA$和$Rt\triangle DGA$中,$\left\{\begin{array}{l}AD = AD\\DF = DG\end{array}\right.$,由$HL$定理得$Rt\triangle DFA\cong Rt\triangle DGA$,则$AF = AG$。
因为$CG = AC+AG$,把$BF = CG$,$AF = AG$代入可得$BF=AC + AF$。
因为$AD$是$\triangle ABC$的外角平分线,$DF\perp AB$,$DG\perp AC$,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$DF = DG$。
又因为$DE$是$BC$的垂直平分线,根据垂直平分线的性质:线段垂直平分线上的点到线段两端的距离相等,所以$DB = DC$。
2. 然后,证明$Rt\triangle DFB\cong Rt\triangle DGC$:
在$Rt\triangle DFB$和$Rt\triangle DGC$中,$\left\{\begin{array}{l}DB = DC\\DF = DG\end{array}\right.$($HL$定理:斜边和一条直角边对应相等的两个直角三角形全等)。
所以$BF = CG$。
3. 接着,证明$Rt\triangle DFA\cong Rt\triangle DGA$:
在$Rt\triangle DFA$和$Rt\triangle DGA$中,$\left\{\begin{array}{l}AD = AD\\DF = DG\end{array}\right.$($HL$定理)。
所以$AF = AG$。
4. 最后,探究$BF$,$AC$,$AF$之间的数量关系:
因为$CG=AC + AG$,又$BF = CG$,$AF = AG$。
解:$BF=AC + AF$。
理由:过点$D$作$DG\perp AC$,交$CA$的延长线于点$G$。
由于$AD$平分$\angle BAG$(外角),$DF\perp AB$,$DG\perp AC$,根据角平分线性质$DF = DG$;又$DE$垂直平分$BC$,所以$DB = DC$。
在$Rt\triangle DFB$和$Rt\triangle DGC$中,$\left\{\begin{array}{l}DB = DC\\DF = DG\end{array}\right.$,由$HL$定理得$Rt\triangle DFB\cong Rt\triangle DGC$,则$BF = CG$。
在$Rt\triangle DFA$和$Rt\triangle DGA$中,$\left\{\begin{array}{l}AD = AD\\DF = DG\end{array}\right.$,由$HL$定理得$Rt\triangle DFA\cong Rt\triangle DGA$,则$AF = AG$。
因为$CG = AC+AG$,把$BF = CG$,$AF = AG$代入可得$BF=AC + AF$。
查看更多完整答案,请扫码查看


