1. 老师布置的作业中有这么一道题:
如图,在△ABC中,D为BC的中点,若AC= 3,AD= 4,则AB的长不可能是( )
A. 5
B. 7
C. 8
D. 9
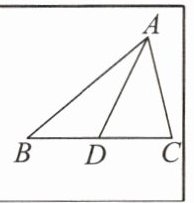
甲同学认为AB,AC,AD这三条边不在同一个三角形中,无法解答,老师给的题目有错误。乙同学认为可以从中点D出发,构造辅助线,利用全等的知识解决。丙同学认为可以过点C作AB的平行线,构造辅助线,利用全等的知识解决。你认为想法正确的是(
A. 甲
B. 乙
C. 丙
D. 乙和丙
如图,在△ABC中,D为BC的中点,若AC= 3,AD= 4,则AB的长不可能是( )
A. 5
B. 7
C. 8
D. 9

甲同学认为AB,AC,AD这三条边不在同一个三角形中,无法解答,老师给的题目有错误。乙同学认为可以从中点D出发,构造辅助线,利用全等的知识解决。丙同学认为可以过点C作AB的平行线,构造辅助线,利用全等的知识解决。你认为想法正确的是(
D
)A. 甲
B. 乙
C. 丙
D. 乙和丙
答案:
D
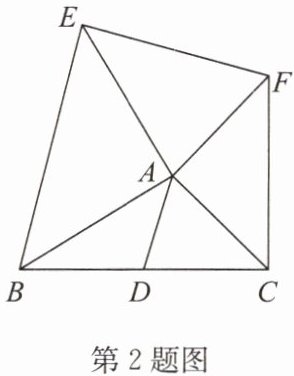
2. 如图,AD是△ABC的中线,AB= AE,AC= AF,∠BAE= ∠CAF= 90°,试判断线段AD与EF的数量关系,并加以证明。

答案:
解:$EF = 2AD$,证明如下:
延长$AD$到$G$,使$DG = AD$,连接$BG$。
因为$AD$是$\triangle ABC$的中线,所以$BD = CD$。
在$\triangle BDG$和$\triangle CDA$中,$\begin{cases}BD = CD\\\angle BDG=\angle CDA\\DG = DA\end{cases}$,根据$SAS$(边角边)定理可得$\triangle BDG\cong\triangle CDA$。
所以$BG = AC$,$\angle GBD=\angle ACD$。
因为$AC = AF$,所以$BG = AF$。
$\angle EAF=\angle BAE+\angle BAC+\angle CAF = 90^{\circ}+\angle BAC + 90^{\circ}=180^{\circ}+\angle BAC$。
$\angle ABG=\angle ABD+\angle GBD=\angle ABD+\angle ACD$,又因为$\angle BAC + \angle ABD+\angle ACD=180^{\circ}$,所以$\angle ABG = 180^{\circ}-\angle BAC$,那么$\angle EAF+\angle ABG=180^{\circ}+\angle BAC + 180^{\circ}-\angle BAC = 360^{\circ}$,$\angle EAB = 90^{\circ}$,$\angle GBA+\angle EAB+\angle EAF+\angle BAF = 360^{\circ}$,可得$\angle EAF+\angle ABG = \angle EAB+\angle BAF+\angle ABG+\angle BAG$,即$\angle EAF=\angle ABG + \angle BAG$(通过角的等量代换)。
又因为$AB = AE$,
在$\triangle ABG$和$\triangle EAF$中,$\begin{cases}AB = AE\\BG = AF\\\angle ABG=\angle EAF\end{cases}$,根据$SAS$(边角边)定理可得$\triangle ABG\cong\triangle EAF$。
所以$EF = AG$,又因为$AG = AD + DG = 2AD$,所以$EF = 2AD$。
延长$AD$到$G$,使$DG = AD$,连接$BG$。
因为$AD$是$\triangle ABC$的中线,所以$BD = CD$。
在$\triangle BDG$和$\triangle CDA$中,$\begin{cases}BD = CD\\\angle BDG=\angle CDA\\DG = DA\end{cases}$,根据$SAS$(边角边)定理可得$\triangle BDG\cong\triangle CDA$。
所以$BG = AC$,$\angle GBD=\angle ACD$。
因为$AC = AF$,所以$BG = AF$。
$\angle EAF=\angle BAE+\angle BAC+\angle CAF = 90^{\circ}+\angle BAC + 90^{\circ}=180^{\circ}+\angle BAC$。
$\angle ABG=\angle ABD+\angle GBD=\angle ABD+\angle ACD$,又因为$\angle BAC + \angle ABD+\angle ACD=180^{\circ}$,所以$\angle ABG = 180^{\circ}-\angle BAC$,那么$\angle EAF+\angle ABG=180^{\circ}+\angle BAC + 180^{\circ}-\angle BAC = 360^{\circ}$,$\angle EAB = 90^{\circ}$,$\angle GBA+\angle EAB+\angle EAF+\angle BAF = 360^{\circ}$,可得$\angle EAF+\angle ABG = \angle EAB+\angle BAF+\angle ABG+\angle BAG$,即$\angle EAF=\angle ABG + \angle BAG$(通过角的等量代换)。
又因为$AB = AE$,
在$\triangle ABG$和$\triangle EAF$中,$\begin{cases}AB = AE\\BG = AF\\\angle ABG=\angle EAF\end{cases}$,根据$SAS$(边角边)定理可得$\triangle ABG\cong\triangle EAF$。
所以$EF = AG$,又因为$AG = AD + DG = 2AD$,所以$EF = 2AD$。
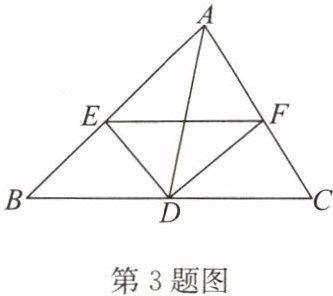
3. 如图,AD是△ABC的中线,点E,F分别在边AB,AC上,且DE⊥DF。求证:BE+CF>EF。

答案:
1. 首先,延长$FD$到点$G$,使$DG = DF$,连接$BG$、$EG$:
因为$AD$是$\triangle ABC$的中线,所以$BD = CD$。
在$\triangle BDG$和$\triangle CDF$中:
$\left\{\begin{array}{l}BD = CD\\\angle BDG=\angle CDF\\DG = DF\end{array}\right.$。
根据$SAS$(边角边)定理,可得$\triangle BDG\cong\triangle CDF$。
由全等三角形的性质可知$BG = CF$。
2. 然后,因为$DE\perp DF$,$DG = DF$:
根据线段垂直平分线的性质(线段垂直平分线上的点到线段两端的距离相等),$DE$是线段$FG$的垂直平分线,所以$EF = EG$。
3. 最后,在$\triangle BEG$中:
根据三角形三边关系(三角形任意两边之和大于第三边),$BE + BG>EG$。
又因为$BG = CF$,$EG = EF$,所以$BE + CF>EF$。
综上,$BE + CF>EF$得证。
因为$AD$是$\triangle ABC$的中线,所以$BD = CD$。
在$\triangle BDG$和$\triangle CDF$中:
$\left\{\begin{array}{l}BD = CD\\\angle BDG=\angle CDF\\DG = DF\end{array}\right.$。
根据$SAS$(边角边)定理,可得$\triangle BDG\cong\triangle CDF$。
由全等三角形的性质可知$BG = CF$。
2. 然后,因为$DE\perp DF$,$DG = DF$:
根据线段垂直平分线的性质(线段垂直平分线上的点到线段两端的距离相等),$DE$是线段$FG$的垂直平分线,所以$EF = EG$。
3. 最后,在$\triangle BEG$中:
根据三角形三边关系(三角形任意两边之和大于第三边),$BE + BG>EG$。
又因为$BG = CF$,$EG = EF$,所以$BE + CF>EF$。
综上,$BE + CF>EF$得证。
查看更多完整答案,请扫码查看


