《2025年启东中学作业本八年级数学上册苏科版盐城专版》

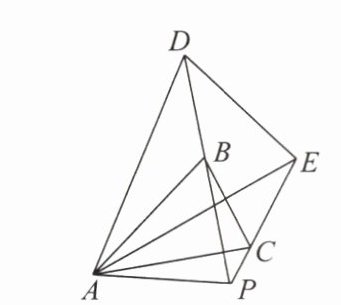
1. 如图,$C为线段AE$上一动点(不与点$A$,$E$重合),在$AE同侧分别作等边三角形ABC和等边三角形CDE$,$AD与BE交于点O$,$AD与BC交于点P$,$BE与CD交于点Q$,连接$PQ$,$OC$.下列结论:①$AD= BE$;②$AP= BQ$;③$PQ// AE$;④$\angle AOB= 60^{\circ}$;⑤$DE= DP$;⑥$OC平分\angle AOE$;⑦$\triangle CPQ$为等边三角形.其中正确的有(C)
A.4个
B.5个
C.6个
D.7个

答案： C

2. 在$\triangle ABC$中,$\angle BAC= 90^{\circ}$,$AB= AC$,$D为BC$的中点.
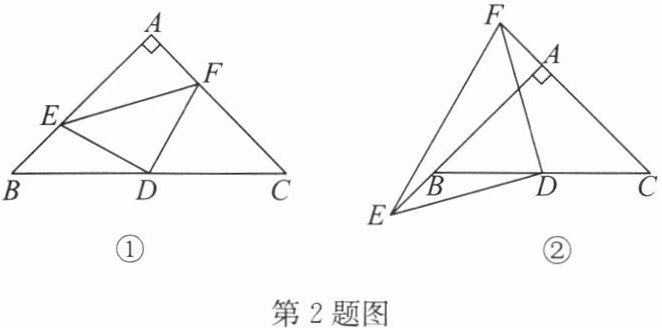
(1)如图①,$E$,$F分别是AB$,$AC$上的点,且$BE= AF$,求证:$\triangle DEF$为等腰直角三角形;
(2)如图②,若$E$,$F分别为AB$,$CA$延长线上的点,仍有$BE= AF$,其他条件不变,那么$\triangle DEF$是否仍为等腰直角三角形? 证明你的结论.

答案：

(1)证明:如答图①，连接AD.
∵AB=AC,∠BAC=90°,D为BC的中点，
∴∠B=45°,AD=$\frac{1}{2}$BC=BD,AD平分∠BAC,∠ADB=90°,
∴∠BAD=∠DAF=45°,
∴∠B=∠DAF.
在△BDE和△ADF中,$\left\{\begin{array}{l} BD=AD,\\ ∠B=∠DAF,\\ BE=AF,\end{array}\right.$
∴△BDE≌△ADF(SAS),
∴DE=DF,∠BDE=∠ADF.
∵∠BDE+∠ADE=90°,
∴∠ADF+∠ADE=90°,
即∠EDF=90°,
∴△DEF为等腰直角三角形.

(2)解:△DEF仍为等腰直角三角形.
证明:如答图②，连接AD.
∵AB=AC,∠BAC=90°,D为BC的中点，
∴∠ABD=45°,AD=$\frac{1}{2}$BC=BD,AD平分∠BAC,∠ADB=90°,
∴∠ABD=∠CAD=45°,
∴∠EBD=∠FAD.
在△BDE和△ADF中,$\left\{\begin{array}{l} BD=AD,\\ ∠EBD=∠FAD,\\ BE=AF,\end{array}\right.$
∴△BDE≌△ADF(SAS),
∴DF=DE,∠BDE=∠ADF.
∵∠ADF+∠FDB=90°,
∴∠BDE+∠FDB=90°,
即∠EDF=90°,
∴△DEF为等腰直角三角形.