1. 如图,在$Rt△ACB$中,$∠C= 90^{\circ },AC= BC$,D 为 AC 边上的点,且$AD= 2CD$,连接BD. 过点 B 作$EB⊥BD$,并截取$EB= DB$,连接 AE 交 CB 于点 F. 有下列结论:①$∠CBE= ∠CDB$;②F 是 AE 的中点;③$∠FEB= ∠FAC+∠CBD$;④$BF= 3CF$. 其中正确的结论共有(
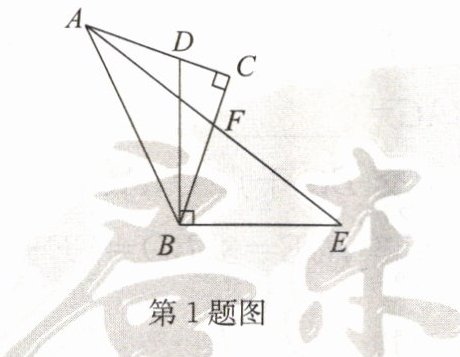
A.1个
B.2个
C.3个
D.4个
C
)
A.1个
B.2个
C.3个
D.4个
答案:
C
2. 如图,一块含$45^{\circ }$角的三角尺的一个顶点 A 与长方形 ABCD($∠BAD= ∠B= ∠C= ∠D= 90^{\circ },AB= CD,AD= BC,AB// CD,AD// BC$)的顶点重合,直角顶点 E 落在边 BC 上,另一个顶点 F 恰好落在边 CD 的中点处,若$BC= 12$,则 AB 的长为____
8
.
答案:
8
3. 如图,在$△ABC$中,$AB= AC$,D,E 是 BC 边上两点,连接 AD,以 AD 为腰作等腰直角$△ADF,∠ADF= 90^{\circ }$,作$FE⊥BC$于点 E,$FE= CE$,连接 CF. 若$BD= 2,CE= 5$,求$△CDF$的面积.
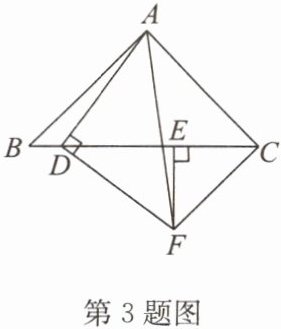

答案:
1. 首先,证明$\triangle ABD\cong\triangle DGF$:
过点$A$作$AG\perp BC$于点$G$。
因为$AB = AC$,$AG\perp BC$,所以$\angle B=\angle ACB$,$BG = CG$。
因为$\angle ADF = 90^{\circ}$,所以$\angle ADG+\angle FDE = 90^{\circ}$,又因为$FE\perp BC$,所以$\angle DFE+\angle FDE = 90^{\circ}$,则$\angle ADG=\angle DFE$。
在$\triangle ADG$和$\triangle DFE$中,$\left\{\begin{array}{l}\angle AGD=\angle DEF = 90^{\circ}\\\angle ADG=\angle DFE\\AD = DF\end{array}\right.$($AD = DF$是等腰直角$\triangle ADF$的腰)。
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ADG\cong\triangle DFE$。
所以$AG = DE$,$DG = EF$。
2. 然后,求$DE$的长度:
已知$BD = 2$,$CE = 5$,设$DE=x$。
因为$BG = CG$,$BG=BD + DG$,$CG=CE+(DE - DG)$(由$DG = EF$且$EF = CE$,所以$DG = CE$)。
则$BD + CE=DE$($BD + DG=CE+(DE - DG)$,把$DG = CE$代入可得)。
所以$DE=BD + CE$,因为$BD = 2$,$CE = 5$,所以$DE=2 + 5=7$。
3. 最后,求$\triangle CDF$的面积:
因为$FE\perp BC$,$FE = CE = 5$,$DE = 7$。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),对于$\triangle CDF$,底$CD=DE + CE=7 + 5=12$,高$EF = 5$。
所以$S_{\triangle CDF}=\frac{1}{2}× CD× EF$。
把$CD = 12$,$EF = 5$代入公式得$S_{\triangle CDF}=\frac{1}{2}×12×5 = 30$。
答:$\triangle CDF$的面积是$30$。
过点$A$作$AG\perp BC$于点$G$。
因为$AB = AC$,$AG\perp BC$,所以$\angle B=\angle ACB$,$BG = CG$。
因为$\angle ADF = 90^{\circ}$,所以$\angle ADG+\angle FDE = 90^{\circ}$,又因为$FE\perp BC$,所以$\angle DFE+\angle FDE = 90^{\circ}$,则$\angle ADG=\angle DFE$。
在$\triangle ADG$和$\triangle DFE$中,$\left\{\begin{array}{l}\angle AGD=\angle DEF = 90^{\circ}\\\angle ADG=\angle DFE\\AD = DF\end{array}\right.$($AD = DF$是等腰直角$\triangle ADF$的腰)。
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ADG\cong\triangle DFE$。
所以$AG = DE$,$DG = EF$。
2. 然后,求$DE$的长度:
已知$BD = 2$,$CE = 5$,设$DE=x$。
因为$BG = CG$,$BG=BD + DG$,$CG=CE+(DE - DG)$(由$DG = EF$且$EF = CE$,所以$DG = CE$)。
则$BD + CE=DE$($BD + DG=CE+(DE - DG)$,把$DG = CE$代入可得)。
所以$DE=BD + CE$,因为$BD = 2$,$CE = 5$,所以$DE=2 + 5=7$。
3. 最后,求$\triangle CDF$的面积:
因为$FE\perp BC$,$FE = CE = 5$,$DE = 7$。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),对于$\triangle CDF$,底$CD=DE + CE=7 + 5=12$,高$EF = 5$。
所以$S_{\triangle CDF}=\frac{1}{2}× CD× EF$。
把$CD = 12$,$EF = 5$代入公式得$S_{\triangle CDF}=\frac{1}{2}×12×5 = 30$。
答:$\triangle CDF$的面积是$30$。
查看更多完整答案,请扫码查看


