《2025年启东中学作业本八年级数学上册苏科版盐城专版》

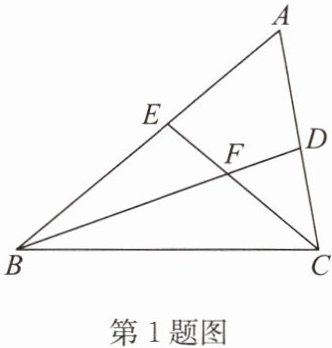
1. 如图,在$\triangle ABC$中,$\angle ABC和\angle ACB的平分线BD$,$CE相交于点F$,$\angle A = 60^{\circ}$.
(1)求$\angle BFC$的度数;
(2)求证:$BC = BE + CD$.

答案：
1.
(1)解:在△ABC中,∠ABC+∠ACB=180°−∠A=180°−60°=120°.
∵∠ABC,∠ACB的平分线BD,CE相交于点F,
∴∠FBC=$\frac{1}{2}$∠ABC,∠FCB=$\frac{1}{2}$∠ACB,
∴∠FBC+∠FCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×120°=60°.
在△BCF中,∠BFC=180°−(∠FBC+∠FCB)=180°−60°=120°.
(2)证明:如答图，在BC上取一点O,使BO=BE,连接OF;
由
(1)知∠BFC=120°,
∴∠BFE=∠CFD=60°.
∵BD,CE分别是∠ABC和∠ACB的平分线,
∴∠ABD=∠DBC,∠ACE=∠BCE.
在△BFE和△BFO中,$\begin{cases} BF=BF, \\ ∠FBE=∠FBO, \\ BE=BO, \end{cases}$
∴△BFE≌△BFO(SAS),
∴∠BFO=∠BFE=60°,
∴∠CFO=∠BFC−∠BFO=60°.
在△OCF和△DCF中,$\begin{cases} ∠CFO=∠CFD, \\ CF=CF, \\ ∠FCO=∠FCD, \end{cases}$
∴△OCF≌△DCF(ASA),
∴CO=CD.
∵BC=BO+CO,
∴BC=BE+CD.

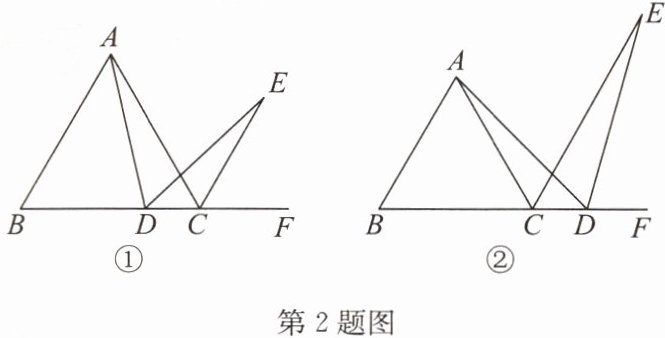
2. 已知$\triangle ABC$为等边三角形,$D为射线BC$上一点,$\angle ADE = 60^{\circ}$,$DE与\triangle ABC的外角\angle ACF的平分线交于点E$.
(1)如图①,若点$D在BC$上,求证:$CA = CD + CE$;
(2)如图②,若点$D在BC$的延长线上,写出$CA$,$CD$,$CE$之间的数量关系,并证明.

答案：
2.
(1)证明:如答图①,在AC上截取CM=CD,连接DM.
∵△ABC是等边三角形,
∴∠ACB=60°,
∴△CDM是等边三角形,
∴MD=CD=CM,∠CMD=∠CDM=60°,
∴∠AMD=120°.
∵∠ADE=60°,
∴∠ADE=∠MDC,
∴∠ADM=∠EDC.
∵∠ACB=60°,
∴∠ACF=120°.
∵DE与∠ACF的平分线交于点E,
∴∠ACE=60°,
∴∠DCE=120°=∠AMD.
在△ADM和△EDC中,$\begin{cases} ∠ADM=∠EDC, \\ MD=CD, \\ ∠AMD=∠ECD, \end{cases}$
∴△ADM≌△EDC(ASA),
∴AM=EC,
∴CA=CM+AM=CD+CE.

(2)解:CA=CE−CD.
证明:如答图②,延长AC到点M,使CM=CD,连接DM.
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠DCM=60°,
∴△CDM是等边三角形,
∴MD=CD=CM,∠CMD=∠CDM=60°.
∵∠ACB=60°,
∴∠ACF=120°.
∵DE与∠ACF的平分线交于点E,
∴∠ACE=∠DCE=60°,
∴∠ECD=∠AMD.
∵∠ADE=60°,
∴∠ADE=∠CDM,
∴∠ADM=∠EDC.
在△ADM和△EDC中,$\begin{cases} ∠ADM=∠EDC, \\ MD=CD, \\ ∠AMD=∠ECD, \end{cases}$
∴△ADM≌△EDC(ASA),
∴AM=EC,
∴CA=AM−CM=CE−CD.