《2025年文轩图书假期生活指导暑七年级数学》

1. 如图,直线$AB// CD$,$GE⊥EF于点E$.若$∠BGE= 60^{\circ}$,则$∠EFD$的度数是 (B)
A.$60^{\circ}$
B.$30^{\circ}$
C.$40^{\circ}$
D.$70^{\circ}$

答案： 解：过点E作EH//AB，
∵AB//CD，
∴EH//CD，
∵GE⊥EF，
∴∠GEF=90°，
∵∠BGE=60°，EH//AB，
∴∠GEH=∠BGE=60°，
∴∠HEF=∠GEF - ∠GEH=90° - 60°=30°，
∵EH//CD，
∴∠EFD=∠HEF=30°。
答案：B

2. 一种路灯的示意图如图所示,其底部支架$AB与吊线FG$平行,灯杆$CD与底部支架AB所成锐角α= 15^{\circ}$,顶部支架$EF与灯杆CD所成锐角β= 45^{\circ}$,则$EF与FG$所成锐角的度数为 (A)
A.$60^{\circ}$
B.$55^{\circ}$
C.$50^{\circ}$
D.$45^{\circ}$

答案： 解：延长FE交AB于点H，
∵AB//FG，
∴EF与FG所成锐角等于EF与AB所成锐角，即∠EHB。
∵∠α=15°，∠β=45°，
∴∠EHB=∠α+∠β=15°+45°=60°。
答案：A

3. 如图,$a// b$,$AB⊥a$,$BC与b$相交,若$∠ABC= 130^{\circ}$,则$∠1= $140°.

答案： 解：过点B作BD//a，
∵a//b，
∴BD//b，
∵AB⊥a，
∴∠ABD=90°，
∵∠ABC=130°，
∴∠DBC=∠ABC - ∠ABD=130° - 90°=40°，
∵BD//b，
∴∠1 + ∠DBC=180°，
∴∠1=180° - 40°=140°。
140°

4. 如图,$∠AEC+∠A= ∠C$,求证:$CD// AB$.

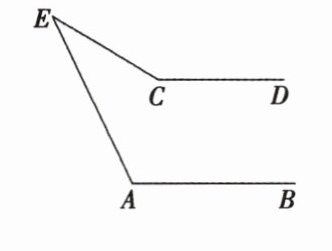
答案：
证明:如图,过点 $E$ 作 $EF // CD$,则 $ \angle C + \angle CEF = 180^{\circ} $.
$ \because \angle AEC + \angle A = \angle C $,且 $ \angle C + \angle CEF = 180^{\circ} $, $ \therefore \angle AEC + \angle A + \angle CEF = 180^{\circ} $,
即 $ \angle AEF + \angle A = 180^{\circ} $, $ \therefore EF // AB $.
$ \because EF // CD $, $ \therefore CD // AB $.

5. [感知]如图1,$AB// CD$,$∠AEP= 40^{\circ}$,$∠PFD= 130^{\circ}$,求$∠EPF$的度数.小明想到了以下方法.
解:如图1,过点$P作PM// AB$,
$\therefore ∠1= ∠AEP= 40^{\circ}$(两直线平行,内错角相等).
$\because AB// CD$(已知),
$\therefore PM// CD$(平行于同一条直线的两直线平行),
$\therefore ∠2+∠PFD= 180^{\circ}$(两直线平行,同旁内角互补).
$\because ∠PFD= 130^{\circ}$(已知),
$\therefore ∠2= 180^{\circ}-130^{\circ}=50^{\circ}$,
$\therefore ∠1+∠2= 40^{\circ}+50^{\circ}=90^{\circ}$,
即$∠EPF= 90^{\circ}$.
[探究]如图2,$AB// CD$,$∠AEP= 50^{\circ}$,$∠PFC= 120^{\circ}$,求$∠EPF$的度数;
[应用]如图3,在[探究]的条件下,$∠PEA的平分线和∠PFC的平分线交于点G$,求$∠G$的度数.

答案：
解:[探究]如图 1,过点 $P$ 作 $PM // AB$,
$ \therefore \angle MPE = \angle AEP = 50^{\circ} $(两直线平行,内错角相等).

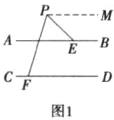
$ \because AB // CD $(已知),
$ \therefore PM // CD $(平行于同一条直线的两直线平行),
$ \therefore \angle MPF = \angle PFC = 120^{\circ} $(两直线平行,内错角相等),
$ \therefore \angle EPF = \angle MPF - \angle MPE = 120^{\circ} - 50^{\circ} = 70^{\circ} $.
[应用]$ \because EG $ 是 $ \angle PEA $ 的平分线, $ FG $ 是 $ \angle PFC $ 的平分线,
$ \therefore \angle AEG = \frac{1}{2} \angle AEP = 25^{\circ} $, $ \angle GFC = \frac{1}{2} \angle PFC = 60^{\circ} $.
如图 2,过点 $G$ 作 $GH // AB$,
$ \therefore \angle HGE = \angle AEG = 25^{\circ} $(两直线平行,内错角相等).
$ \because AB // CD $(已知),
$ \therefore GH // CD $(平行于同一条直线的两直线平行),
$ \therefore \angle HGF = \angle GFC = 60^{\circ} $(两直线平行,内错角相等),
$ \therefore \angle AGB = \angle HGF - \angle HGE = 60^{\circ} - 25^{\circ} = 35^{\circ} $.