《2025年文轩图书假期生活指导暑七年级数学》

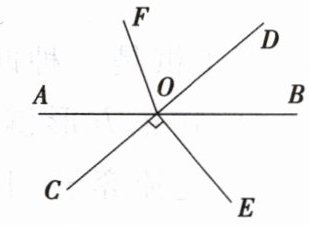
20. 如图,已知直线$AB与CD相交于点O$,$EO\perp CD于点O$,$OF平分\angle AOD$,且$\angle BOE= 50^{\circ}$,求$\angle COF$的度数.

答案： 解：$\because EO\perp CD$，
$\therefore \angle DOE=90^{\circ}$，
$\because \angle BOE=50^{\circ}$，
$\therefore \angle BOD=\angle DOE - \angle BOE=90^{\circ}-50^{\circ}=40^{\circ}$，
$\because \angle AOC$与$\angle BOD$是对顶角，
$\therefore \angle AOC=\angle BOD=40^{\circ}$，
$\because \angle AOD + \angle BOD=180^{\circ}$，
$\therefore \angle AOD=180^{\circ}-\angle BOD=180^{\circ}-40^{\circ}=140^{\circ}$，
$\because OF$平分$\angle AOD$，
$\therefore \angle AOF=\frac{1}{2}\angle AOD=\frac{1}{2}×140^{\circ}=70^{\circ}$，
$\therefore \angle COF=\angle AOC + \angle AOF=40^{\circ}+70^{\circ}=110^{\circ}$。

21. 春天到了,七年级同学到人民公园春游,张华对着景区示意图(如图所示)描述音乐台和牡丹园的位置(图中小正方形的边长是$100m$长),音乐台的坐标是$(200,500)$,牡丹园的坐标是$(500,400)$.

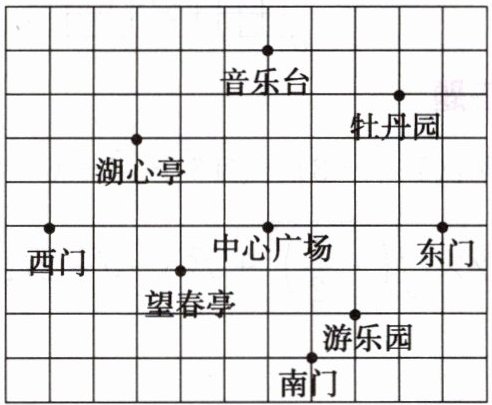
(1)请你在景区示意图上画出张华建立的平面直角坐标系；
(2)用张华建立的平面直角坐标系,描述公园内其他景点的坐标.

答案：
解：
(1) 张华建立的平面直角坐标系如图所示：
(2) 中心广场$(200,100)$；南门$(300,-200)$；东门$(600,100)$；游乐园$(400,-100)$；望春亭$(0,0)$；西门$(-300,100)$；湖心亭$(-100,300)$。

22. 如图,四边形$ABCD$中,点$E$,$F分别在AD$,$BC$上,$G在AB$的延长线上,若$\angle D+\angle GBC= 180^{\circ}$,$AD// BC$,$EF// DC$. 求证：$AB// EF$.

答案： 证明：$\because AD// BC$，
$\therefore \angle A = \angle GBC$（两直线平行，同位角相等）。
$\because \angle D + \angle GBC = 180^{\circ}$，
$\therefore \angle A + \angle D = 180^{\circ}$（等量代换）。
$\therefore DC// AB$（同旁内角互补，两直线平行）。
$\because EF// DC$，
$\therefore AB// EF$（平行于同一条直线的两条直线平行）。

23. 下面是解答一道几何题时两种添加辅助线的方法,选择其中一种,完成证明.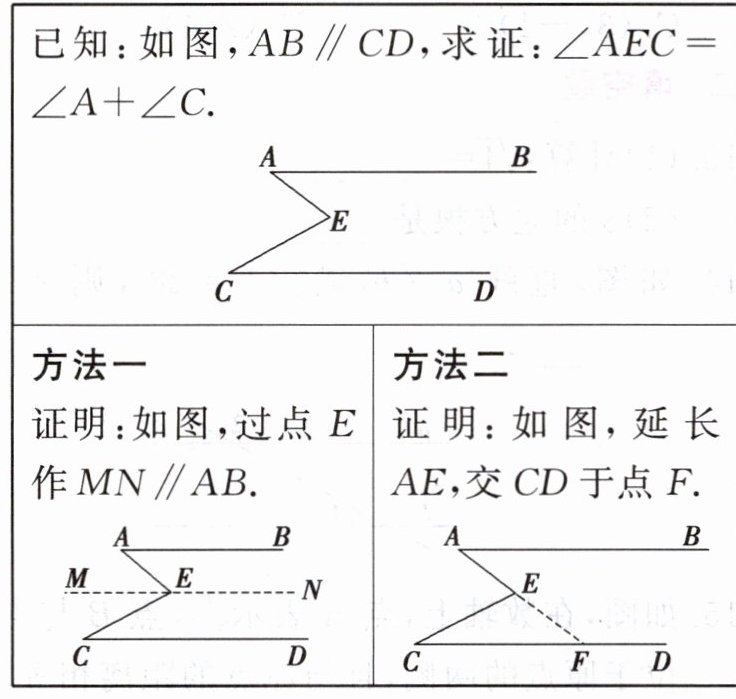

答案： 方法一
证明：如图，过点 E 作 $ MN // AB $。
∵ $ AB // CD $，
∴ $ AB // CD // MN $，
∴ $ \angle A = \angle AEM $（两直线平行，内错角相等），
$ \angle C = \angle CEM $（两直线平行，内错角相等），
∵ $ \angle AEC = \angle AEM + \angle CEM $，
∴ $ \angle AEC = \angle A + \angle C $。
方法二
证明：如图，延长 AE，交 CD 于点 F。
∵ $ AB // CD $，
∴ $ \angle A = \angle AFC $（两直线平行，内错角相等），
∵ $ \angle AEC = \angle AFC + \angle C $（三角形的一个外角等于与它不相邻的两个内角的和），
∴ $ \angle AEC = \angle A + \angle C $。