《2025年文轩图书假期生活指导暑七年级数学》

1. 根据“$x$的 3 倍与 2 的和不大于 10”列出的不等式是(A)
A.$3x+2\leqslant 10$
B.$3x+2\geqslant 10$
C.$3x+2＜10$
D.$3x+2＞10$

答案： 解：“x的3倍”表示为3x，“与2的和”表示为3x+2，“不大于10”即“≤10”，所以列出的不等式是3x+2≤10。
答案：A

2. 如图是某桥洞的限高标志,则能通过此桥洞的车辆高度是(D)
A.6.5 m
B.6 m
C.5.5 m
D.4.5 m

答案： 解：由限高标志可知桥洞限高5m，车辆高度需小于5m。选项中只有4.5m＜5m，故能通过此桥洞的车辆高度是4.5m。
答案：D

3. 下列数中,能使不等式$5x-1＜6成立的x$的值为(A)
A.1
B.2
C.3
D.4

答案： 解：解不等式$5x - 1 ＜ 6$，
移项得$5x ＜ 6 + 1$，
合并同类项得$5x ＜ 7$，
系数化为$1$得$x ＜ \frac{7}{5} = 1.4$。
选项中只有$1 ＜ 1.4$，所以能使不等式成立的$x$的值为$1$。
A

4. 下列判断不正确的是(C)
A.若$a＞b$,则$-4a＜-4b$
B.若$2a＞3a$,则$a＜0$
C.若$a＞b$,则$ac^{2}＞bc^{2}$
D.若$ac^{2}＞bc^{2}$,则$a＞b$

答案： 解：A. 若$a＞b$，不等式两边同时乘以$-4$，不等号方向改变，得$-4a＜-4b$，正确。
B. 若$2a＞3a$，移项得$2a - 3a＞0$，即$-a＞0$，则$a＜0$，正确。
C. 若$a＞b$，当$c = 0$时，$c^2 = 0$，则$ac^2 = bc^2 = 0$，此时$ac^2＞bc^2$不成立，错误。
D. 若$ac^2＞bc^2$，因为$c^2≥0$，且$ac^2＞bc^2$，所以$c^2＞0$，不等式两边同时除以$c^2$，不等号方向不变，得$a＞b$，正确。
结论：不正确的是C。
答案：C

5. 下列不等式中,与$-x＞1$组成的不等式组无解的是(A)
A.$x＞2$
B.$x＜0$
C.$x＜-2$
D.$x＞-3$

答案： 解：由$-x＞1$，得$x＜-1$。
A. 不等式组为$\left\{\begin{array}{l}x＜-1\\x＞2\end{array}\right.$，无解；
B. 不等式组为$\left\{\begin{array}{l}x＜-1\\x＜0\end{array}\right.$，解集为$x＜-1$；
C. 不等式组为$\left\{\begin{array}{l}x＜-1\\x＜-2\end{array}\right.$，解集为$x＜-2$；
D. 不等式组为$\left\{\begin{array}{l}x＜-1\\x＞-3\end{array}\right.$，解集为$-3＜x＜-1$。
A

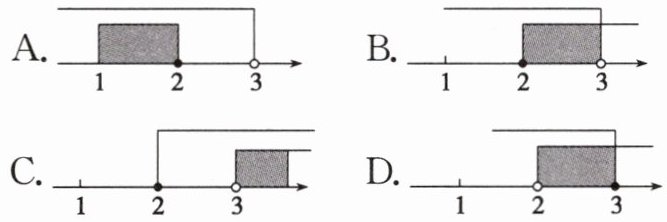
6. 不等式组$\left\{\begin{array}{l} 3x-2＜2x+1\\ x\geqslant 2\end{array} \right. $的解集在数轴上表示为(B)

A.
B.
C.
D.

答案： 解不等式组：
1. 解不等式 $3x - 2 ＜ 2x + 1$，得 $x ＜ 3$。
2. 不等式 $x \geq 2$ 解集为 $x \geq 2$。
3. 不等式组解集为 $2 \leq x ＜ 3$。
在数轴上表示为从2（实心点）向右到3（空心点）的线段。
答案：B

7. 已知实数$a,b满足a-b+1= 0$,$0＜a+b+1＜1$,则下列判断正确的是(C)
A.$-\frac {1}{2}＜a＜0$
B.$\frac {1}{2}＜b＜1$
C.$-2＜2a+4b＜1$
D.$-1＜4a+2b＜0$

答案： 解：由$a - b + 1 = 0$得$b = a + 1$。
将$b = a + 1$代入$0 ＜ a + b + 1 ＜ 1$，得：
$0 ＜ a + (a + 1) + 1 ＜ 1$
$0 ＜ 2a + 2 ＜ 1$
$-2 ＜ 2a ＜ -1$
$-1 ＜ a ＜ -\frac{1}{2}$，故A错误。
$b = a + 1$，则$0 ＜ b ＜ \frac{1}{2}$，故B错误。
$2a + 4b = 2a + 4(a + 1) = 6a + 4$，
$\because -1 ＜ a ＜ -\frac{1}{2}$，$\therefore -6 ＜ 6a ＜ -3$，$-2 ＜ 6a + 4 ＜ 1$，故C正确。
$4a + 2b = 4a + 2(a + 1) = 6a + 2$，
$\because -1 ＜ a ＜ -\frac{1}{2}$，$\therefore -6 ＜ 6a ＜ -3$，$-4 ＜ 6a + 2 ＜ -1$，故D错误。
答案：C

8. 关于$x,y的方程组\left\{\begin{array}{l} 2x-y= 2k-3,\\ x-2y= k\end{array} \right. 的解中x与y$的和不小于 5,则$k$的取值范围为(A)
A.$k\geqslant 8$
B.$k＞8$
C.$k\leqslant 8$
D.$k＜8$

答案： 解：解方程组$\left\{\begin{array}{l} 2x - y = 2k - 3 \\ x - 2y = k \end{array}\right.$
由$x - 2y = k$得$x = k + 2y$，代入$2x - y = 2k - 3$：
$2(k + 2y) - y = 2k - 3$
$2k + 4y - y = 2k - 3$
$3y = -3$
$y = -1$
将$y = -1$代入$x = k + 2y$得$x = k - 2$
$x + y = (k - 2) + (-1) = k - 3$
因为$x + y \geq 5$，所以$k - 3 \geq 5$，解得$k \geq 8$
A

9. 关于$x的不等式组\left\{\begin{array}{l} x＞m+3,\\ 5x-2＜4x+1\end{array} \right. $的整数解仅有 4 个,则$m$的取值范围是(A)
A.$-5\leqslant m＜-4$
B.$-5＜m\leqslant -4$
C.$-4\leqslant m＜-3$
D.$-4＜m\leqslant -3$

答案： 解：解不等式组$\left\{\begin{array}{l} x ＞ m + 3\\5x - 2 ＜ 4x + 1\end{array}\right.$
解第二个不等式：$5x - 2 ＜ 4x + 1$，得$x ＜ 3$
所以不等式组的解集为$m + 3 ＜ x ＜ 3$
因为整数解仅有4个，所以整数解为$2,1,0,-1$
则$-2 \leq m + 3 ＜ -1$
解得$-5 \leq m ＜ -4$
答案：A

10. 小玲搭飞机旅游,已知她搭飞机产生的碳排放量为 800 kg,为了弥补这些碳排放量,她决定上下班时从驾驶汽车改成搭公交车.依据下图的信息,假设小玲每日上下班驾驶汽车或搭公交车的来回总距离皆为20 km,则与驾驶汽车相比,她至少要改搭公交车上下班几天,减少产生的碳排放量才会超过她搭飞机产生的碳排放量?
(C)
A.310 天
B.309 天
C.308 天
D.307 天

答案： 解：设小玲至少要改搭公交车上下班 $ x $ 天。
汽车每日上下班碳排放量：$ 20 × 0.17 = 3.4 \, \text{kg} $
公交车每日上下班碳排放量：$ 20 × 0.04 = 0.8 \, \text{kg} $
每日减少碳排放量：$ 3.4 - 0.8 = 2.6 \, \text{kg} $
依题意列不等式：$ 2.6x ＞ 800 $
解得：$ x ＞ \frac{800}{2.6} \approx 307.69 $
$ x $ 取最小整数为 308。
答：C

11. 如图,在数轴上表示$x$的取值范围是$x＞2$.

答案： $x＞2$

12. 不等式组$\left\{\begin{array}{l} x+2＞3\\ 3x-8＜1\end{array} \right. $的解集是$1＜x＜3$.

答案： 解：解不等式$x + 2＞3$，得$x＞1$；
解不等式$3x - 8＜1$，得$3x＜9$，即$x＜3$；
所以不等式组的解集是$1＜x＜3$。

13. 不等式组$\left\{\begin{array}{l} x＞\frac {x-2}{2}\\ 5x-3＜9+x\end{array} \right. $的整数解有4个.

答案： 解：解不等式 $x ＞ \frac{x - 2}{2}$，两边同乘2得：$2x ＞ x - 2$，移项得：$2x - x ＞ -2$，解得 $x ＞ -2$。
解不等式 $5x - 3 ＜ 9 + x$，移项得：$5x - x ＜ 9 + 3$，合并同类项得：$4x ＜ 12$，解得 $x ＜ 3$。
所以不等式组的解集为 $-2 ＜ x ＜ 3$。
其整数解为 $-1, 0, 1, 2$，共4个。
4