2025年文轩图书假期生活指导暑七年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年文轩图书假期生活指导暑七年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 定义新运算:
①在平面直角坐标系中,$\{a,b\}$表示动点从原点出发,沿着$x轴正方向(a\geq0)或负方向(a\lt0)平移\vert a\vert$个单位长度,再沿着$y轴正方向(b\geq0)或负方向(b\lt0)平移\vert b\vert$个单位长度。例如,动点从原点出发,沿着$x轴负方向平移2$个单位长度,再沿着$y轴正方向平移1$个单位长度,记作$(-2,1)$。
②加法运算法则:$\{a,b\}+\{c,d\}= \{a + c,b + d\}$,其中$a,b,c,d$为实数。
若$\{3,5\}+\{m,n\}= \{-1,2\}$,则下列结论正确的是(
A.$m = 2$,$n = 7$
B.$m = -4$,$n = -3$
C.$m = 4$,$n = 3$
D.$m = -4$,$n = 3$
①在平面直角坐标系中,$\{a,b\}$表示动点从原点出发,沿着$x轴正方向(a\geq0)或负方向(a\lt0)平移\vert a\vert$个单位长度,再沿着$y轴正方向(b\geq0)或负方向(b\lt0)平移\vert b\vert$个单位长度。例如,动点从原点出发,沿着$x轴负方向平移2$个单位长度,再沿着$y轴正方向平移1$个单位长度,记作$(-2,1)$。
②加法运算法则:$\{a,b\}+\{c,d\}= \{a + c,b + d\}$,其中$a,b,c,d$为实数。
若$\{3,5\}+\{m,n\}= \{-1,2\}$,则下列结论正确的是(
B
)A.$m = 2$,$n = 7$
B.$m = -4$,$n = -3$
C.$m = 4$,$n = 3$
D.$m = -4$,$n = 3$
答案:
解:根据新运算加法法则,$\{3,5\}+\{m,n\}=\{3+m,5+n\}$。
已知$\{3,5\}+\{m,n\}=\{-1,2\}$,则可得:
$3 + m = -1$,解得$m = -1 - 3 = -4$;
$5 + n = 2$,解得$n = 2 - 5 = -3$。
结论:$m=-4$,$n=-3$,选B。
已知$\{3,5\}+\{m,n\}=\{-1,2\}$,则可得:
$3 + m = -1$,解得$m = -1 - 3 = -4$;
$5 + n = 2$,解得$n = 2 - 5 = -3$。
结论:$m=-4$,$n=-3$,选B。
11. 在平面直角坐标系中,点$P(-3,-2)$所在的象限是第
三
象限。
答案:
解:在平面直角坐标系中,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)。
点$P(-3,-2)$的横坐标为$-3$(负数),纵坐标为$-2$(负数),符合第三象限(-,-)的特征。
三
点$P(-3,-2)$的横坐标为$-3$(负数),纵坐标为$-2$(负数),符合第三象限(-,-)的特征。
三
12. 观察如图所示的象棋棋盘,若“兵”所在的位置用$(1,3)$表示,“炮”所在的位置用$(5,4)$表示,那么“帅”所在的位置可表示为______。
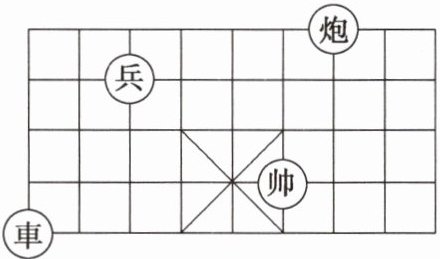

(4,1)
答案:
解:由“兵”$(1,3)$和“炮”$(5,4)$可知,数对中第一个数表示列数,第二个数表示行数。
观察棋盘,“帅”在第4列,第1行,所以“帅”所在的位置可表示为$(4,1)$。
$(4,1)$
观察棋盘,“帅”在第4列,第1行,所以“帅”所在的位置可表示为$(4,1)$。
$(4,1)$
13. 在平面直角坐标系中,线段$AB的端点坐标分别为A(2,-1)$,$B(1,0)$,将线段$AB$平移后,点$A的对应点A'的坐标为(2,1)$,则点$B的对应点B'$的坐标为
(1,2)
。
答案:
解:线段AB平移后,点A(2,-1)的对应点A'的坐标为(2,1)。
平移规律为:横坐标不变,纵坐标增加2。
则点B(1,0)的对应点B'的坐标为(1,0+2)=(1,2)。
答案:(1,2)
平移规律为:横坐标不变,纵坐标增加2。
则点B(1,0)的对应点B'的坐标为(1,0+2)=(1,2)。
答案:(1,2)
14. 已知点$P(2m - 1,4 - m)在过点A(2,3)$,且与$x$轴平行的直线上,则$P$点坐标为
(1,3)
。
答案:
解:因为与x轴平行的直线上的点纵坐标相等,点A(2,3)在此直线上,所以该直线的解析式为y=3。
点P(2m - 1,4 - m)在这条直线上,所以4 - m = 3,解得m = 1。
将m = 1代入2m - 1,得2×1 - 1 = 1。
所以P点坐标为(1,3)。
(1,3)
点P(2m - 1,4 - m)在这条直线上,所以4 - m = 3,解得m = 1。
将m = 1代入2m - 1,得2×1 - 1 = 1。
所以P点坐标为(1,3)。
(1,3)
15. 如图,在平面直角坐标系中,一动点从原点$O$出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点$A_{1}(0,1)$,$A_{2}(1,1)$,$A_{3}(1,0)$,$A_{4}(2,0)$,…那么点$A_{2020}$的坐标为______
(1010,0)
。
答案:
解:观察点的坐标规律:
$A_1(0,1)$,$A_2(1,1)$,$A_3(1,0)$,$A_4(2,0)$,
$A_5(2,1)$,$A_6(3,1)$,$A_7(3,0)$,$A_8(4,0)$,…
每4个点为一个循环组,循环组内点的坐标依次为$(n,1)$,$(n+1,1)$,$(n+1,0)$,$(n+2,0)$($n$为循环组起始横坐标)。
$2020÷4=505$,刚好整除,说明$A_{2020}$是第505个循环组的第4个点。
每个循环组第4个点的坐标为$(2×505,0)=(1010,0)$。
故点$A_{2020}$的坐标为$(1010,0)$。
$A_1(0,1)$,$A_2(1,1)$,$A_3(1,0)$,$A_4(2,0)$,
$A_5(2,1)$,$A_6(3,1)$,$A_7(3,0)$,$A_8(4,0)$,…
每4个点为一个循环组,循环组内点的坐标依次为$(n,1)$,$(n+1,1)$,$(n+1,0)$,$(n+2,0)$($n$为循环组起始横坐标)。
$2020÷4=505$,刚好整除,说明$A_{2020}$是第505个循环组的第4个点。
每个循环组第4个点的坐标为$(2×505,0)=(1010,0)$。
故点$A_{2020}$的坐标为$(1010,0)$。
16. 现有一张利用平面直角坐标系画出来的某公园景区地图,如图, 若知道点$F的坐标为(0,0)$,游乐园$D的坐标为(2,-2)$。
若知道点$F的坐标为(0,0)$,游乐园$D的坐标为(2,-2)$。
(1)请按题意建立平面直角坐标系,在图中画出来;
(2)写出其他四个景点的坐标。
 若知道点$F的坐标为(0,0)$,游乐园$D的坐标为(2,-2)$。
若知道点$F的坐标为(0,0)$,游乐园$D的坐标为(2,-2)$。(1)请按题意建立平面直角坐标系,在图中画出来;
(2)写出其他四个景点的坐标。
答案:
解:
(1)构建直角坐标系如下:

(2)根据游乐园D的坐标为(2,-2),可知图中的每个方格的长度为1,结合直角坐标系可知:音乐台A的坐标为(0,4),湖心亭B的坐标为(-3,2),望春亭C的坐标为(-2,-1),牡丹园E的坐标为(3,3)。
解:
(1)构建直角坐标系如下:

(2)根据游乐园D的坐标为(2,-2),可知图中的每个方格的长度为1,结合直角坐标系可知:音乐台A的坐标为(0,4),湖心亭B的坐标为(-3,2),望春亭C的坐标为(-2,-1),牡丹园E的坐标为(3,3)。
17. 平面直角坐标系上有一点$P(2a - 4,a + 3)$,请根据题意回答下列问题:
(1)若点$P在x$轴上,求出点$P$的坐标;
(2)点$Q的坐标为(6,-1)且PQ// y$轴,求出点$P$的坐标;
(3)若点$P到y轴的距离为2$,直接写出$a$的值。
(1)若点$P在x$轴上,求出点$P$的坐标;
(2)点$Q的坐标为(6,-1)且PQ// y$轴,求出点$P$的坐标;
(3)若点$P到y轴的距离为2$,直接写出$a$的值。
答案:
解:
(1)
∵点P(2a - 4,a + 3)在x轴上,
∴a + 3 = 0,解得a = -3,
∴2a - 4 = 2×(-3) - 4 = -10,
∴点P的坐标为(-10,0)。
(2)
∵PQ//y轴,
∴2a - 4 = 6,
解得a = 5,
∴a + 3 = 5 + 3 = 8,
∴点P的坐标为(6,8)。
(3)a的值为3或1。
解析:
∵点P到y轴的距离为2,
∴|2a - 4| = 2,
∴2a - 4 = 2,或2a - 4 = -2,
解得a = 3,或a = 1。
(1)
∵点P(2a - 4,a + 3)在x轴上,
∴a + 3 = 0,解得a = -3,
∴2a - 4 = 2×(-3) - 4 = -10,
∴点P的坐标为(-10,0)。
(2)
∵PQ//y轴,
∴2a - 4 = 6,
解得a = 5,
∴a + 3 = 5 + 3 = 8,
∴点P的坐标为(6,8)。
(3)a的值为3或1。
解析:
∵点P到y轴的距离为2,
∴|2a - 4| = 2,
∴2a - 4 = 2,或2a - 4 = -2,
解得a = 3,或a = 1。
查看更多完整答案,请扫码查看


