2025年文轩图书假期生活指导暑七年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年文轩图书假期生活指导暑七年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 实数$a,b,c,d$在数轴上对应点的位置如图,其中有一对互为相反数,它们是 (
A.$a与d$
B.$b与d$
C.$c与d$
D.$a与c$
C
)A.$a与d$
B.$b与d$
C.$c与d$
D.$a与c$
答案:
解:由数轴可知,点c在原点左侧,点d在原点右侧,且c到原点的距离与d到原点的距离相等,所以c与d互为相反数。
答案:C
答案:C
2. 如图,数轴上点$A,B,C,D分别对应实数a,b,c,d$,下列各式的值最小的是 (
A.$|a|$
B.$|b|$
C.$|c|$
D.$|d|$
C
)A.$|a|$
B.$|b|$
C.$|c|$
D.$|d|$
答案:
由数轴可知:点A、B在原点左侧,点C、D在原点右侧。
点A到原点的距离大于点B到原点的距离,即$|a| > |b|$;
点C到原点的距离小于点D到原点的距离,即$|c| < |d|$;
且点B到原点的距离大于点C到原点的距离,即$|b| > |c|$。
综上可得$|a| > |b| > |c| < |d|$,所以各式的值最小的是$|c|$。
C
点A到原点的距离大于点B到原点的距离,即$|a| > |b|$;
点C到原点的距离小于点D到原点的距离,即$|c| < |d|$;
且点B到原点的距离大于点C到原点的距离,即$|b| > |c|$。
综上可得$|a| > |b| > |c| < |d|$,所以各式的值最小的是$|c|$。
C
3. 实数$a,b,c$在数轴上的位置如图所示,下列结论正确的是 (
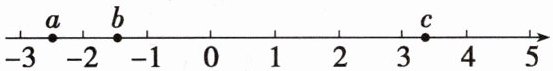
A.$b+c>3$
B.$a-c<0$
C.$|a|>|c|$
D.$-2a<-2b$
B
)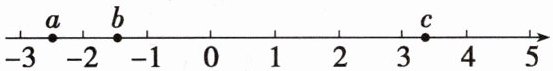
A.$b+c>3$
B.$a-c<0$
C.$|a|>|c|$
D.$-2a<-2b$
答案:
由数轴可知:$a\approx -2.5$,$b\approx -1.5$,$c\approx 3.5$。
A. $b + c\approx -1.5 + 3.5 = 2$,$2 < 3$,故A错误;
B. $a - c\approx -2.5 - 3.5 = -6 < 0$,故B正确;
C. $|a| = 2.5$,$|c| = 3.5$,$2.5 < 3.5$,故C错误;
D. $-2a = 5$,$-2b = 3$,$5 > 3$,故D错误。
结论:B
A. $b + c\approx -1.5 + 3.5 = 2$,$2 < 3$,故A错误;
B. $a - c\approx -2.5 - 3.5 = -6 < 0$,故B正确;
C. $|a| = 2.5$,$|c| = 3.5$,$2.5 < 3.5$,故C错误;
D. $-2a = 5$,$-2b = 3$,$5 > 3$,故D错误。
结论:B
4. 已知实数$a,b,c$在数轴上对应点如图所示,其中$a与c$互为相反数,化简:$|b-c|-|a+c|-|a+b|= $
$a + c$
.
答案:
由数轴可得:$a < b < c$,且$|a| > |b|$。
因为$a$与$c$互为相反数,所以$a + c = 0$。
因为$b < c$,所以$b - c < 0$,则$|b - c| = c - b$。
因为$a + c = 0$,所以$|a + c| = 0$。
因为$a < 0$,$b > 0$,且$|a| > |b|$,所以$a + b < 0$,则$|a + b| = - (a + b) = -a - b$。
所以$|b - c| - |a + c| - |a + b| = (c - b) - 0 - (-a - b) = c - b + a + b = a + c$。
故答案为:$a + c$。
因为$a$与$c$互为相反数,所以$a + c = 0$。
因为$b < c$,所以$b - c < 0$,则$|b - c| = c - b$。
因为$a + c = 0$,所以$|a + c| = 0$。
因为$a < 0$,$b > 0$,且$|a| > |b|$,所以$a + b < 0$,则$|a + b| = - (a + b) = -a - b$。
所以$|b - c| - |a + c| - |a + b| = (c - b) - 0 - (-a - b) = c - b + a + b = a + c$。
故答案为:$a + c$。
5. 如图,一只蚂蚁从点$A沿数轴向右爬2\sqrt{2}个单位长度后到达点B$,点$A表示-\sqrt{2}$,设点$B所表示的数为m$.
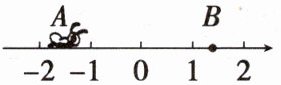
(1) 求$m$的值;
(2) 求$|m-2\sqrt{2}|+(m-\sqrt{2})^{2}$的值.
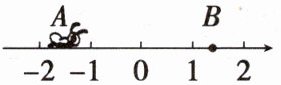
(1) 求$m$的值;
(2) 求$|m-2\sqrt{2}|+(m-\sqrt{2})^{2}$的值.
答案:
解:
(1) $ m = -\sqrt{2} + 2\sqrt{2} = \sqrt{2} $;
(2) 当 $ m = \sqrt{2} $ 时, 原式 $ = |\sqrt{2} - 2\sqrt{2}| + (\sqrt{2} - \sqrt{2})^2 = \sqrt{2} $.
(1) $ m = -\sqrt{2} + 2\sqrt{2} = \sqrt{2} $;
(2) 当 $ m = \sqrt{2} $ 时, 原式 $ = |\sqrt{2} - 2\sqrt{2}| + (\sqrt{2} - \sqrt{2})^2 = \sqrt{2} $.
6. 如图,数轴上从左至右依次有$C,O,A,B$四个点,分别对应的数字为$x,0,1和\sqrt{3}$,且$AB= CO$.

(1) 求$AB$的长,并求$x$的值;
(2) 求$(x+\sqrt{3})^{2}$的平方根.

(1) 求$AB$的长,并求$x$的值;
(2) 求$(x+\sqrt{3})^{2}$的平方根.
答案:
解:
(1) $ \because A, B $ 对应的数字为 $ 1 $ 和 $ \sqrt{3} $, $ \therefore AB = \sqrt{3} - 1 $,
$ \because C, O $ 对应的数字为 $ x, 0 $, $ \therefore CO = 0 - x = -x $,
$ \because AB = CO $, $ \therefore \sqrt{3} - 1 = -x $, $ \therefore x = 1 - \sqrt{3} $;
(2) 当 $ x = 1 - \sqrt{3} $ 时, $ (x + \sqrt{3})^2 = (1 - \sqrt{3} + \sqrt{3})^2 = 1^2 = 1 $,
$ \because 1 $ 的平方根是 $ \pm 1 $, $ \therefore (x + \sqrt{3})^2 $ 的平方根是 $ \pm 1 $.
(1) $ \because A, B $ 对应的数字为 $ 1 $ 和 $ \sqrt{3} $, $ \therefore AB = \sqrt{3} - 1 $,
$ \because C, O $ 对应的数字为 $ x, 0 $, $ \therefore CO = 0 - x = -x $,
$ \because AB = CO $, $ \therefore \sqrt{3} - 1 = -x $, $ \therefore x = 1 - \sqrt{3} $;
(2) 当 $ x = 1 - \sqrt{3} $ 时, $ (x + \sqrt{3})^2 = (1 - \sqrt{3} + \sqrt{3})^2 = 1^2 = 1 $,
$ \because 1 $ 的平方根是 $ \pm 1 $, $ \therefore (x + \sqrt{3})^2 $ 的平方根是 $ \pm 1 $.
查看更多完整答案,请扫码查看


