2025年暑假作业北京教育出版社五年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业北京教育出版社五年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 口算。
$\frac {2}{5}+\frac {7}{10}=$
$\frac {11}{18}+\frac {7}{18}=$
$\frac {1}{7}+\frac {2}{14}=$
$\frac {1}{4}+\frac {1}{8}+\frac {1}{16}=$
$\frac {2}{5}+\frac {7}{10}=$
$1\frac{1}{10}$
$\frac {5}{6}-\frac {2}{3}=$$\frac{1}{6}$
$\frac {11}{18}+\frac {7}{18}=$
$1$
$45-\frac {5}{9}=$$44\frac{4}{9}$
$\frac {1}{7}+\frac {2}{14}=$
$\frac{2}{7}$
$\frac {1}{2}-\frac {1}{5}=$$\frac{3}{10}$
$\frac {1}{4}+\frac {1}{8}+\frac {1}{16}=$
$\frac{7}{16}$
$1-\frac {1}{5}-\frac {1}{10}=$$\frac{7}{10}$
答案:
【解析】:
1. 计算$\frac{2}{5}+\frac{7}{10}$:
先通分,$\frac{2}{5}=\frac{2×2}{5×2}=\frac{4}{10}$,则$\frac{2}{5}+\frac{7}{10}=\frac{4}{10}+\frac{7}{10}=\frac{4 + 7}{10}=\frac{11}{10}=1\frac{1}{10}$。
2. 计算$\frac{5}{6}-\frac{2}{3}$:
先通分,$\frac{2}{3}=\frac{2×2}{3×2}=\frac{4}{6}$,则$\frac{5}{6}-\frac{2}{3}=\frac{5}{6}-\frac{4}{6}=\frac{5 - 4}{6}=\frac{1}{6}$。
3. 计算$\frac{11}{18}+\frac{7}{18}$:
同分母分数相加,分母不变,分子相加,$\frac{11}{18}+\frac{7}{18}=\frac{11 + 7}{18}=\frac{18}{18}=1$。
4. 计算$45-\frac{5}{9}$:
把$45$写成$44+\frac{9}{9}$,则$45-\frac{5}{9}=44+\frac{9}{9}-\frac{5}{9}=44+\frac{9 - 5}{9}=44\frac{4}{9}$。
5. 计算$\frac{1}{7}+\frac{2}{14}$:
先化简$\frac{2}{14}=\frac{1}{7}$,则$\frac{1}{7}+\frac{2}{14}=\frac{1}{7}+\frac{1}{7}=\frac{1+1}{7}=\frac{2}{7}$。
6. 计算$\frac{1}{2}-\frac{1}{5}$:
先通分,$\frac{1}{2}=\frac{1×5}{2×5}=\frac{5}{10}$,$\frac{1}{5}=\frac{1×2}{5×2}=\frac{2}{10}$,则$\frac{1}{2}-\frac{1}{5}=\frac{5}{10}-\frac{2}{10}=\frac{5 - 2}{10}=\frac{3}{10}$。
7. 计算$\frac{1}{4}+\frac{1}{8}+\frac{1}{16}$:
先通分,$\frac{1}{4}=\frac{1×4}{4×4}=\frac{4}{16}$,$\frac{1}{8}=\frac{1×2}{8×2}=\frac{2}{16}$,则$\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=\frac{4}{16}+\frac{2}{16}+\frac{1}{16}=\frac{4 + 2+1}{16}=\frac{7}{16}$。
8. 计算$1-\frac{1}{5}-\frac{1}{10}$:
先把$1$写成$\frac{10}{10}$,$\frac{1}{5}=\frac{1×2}{5×2}=\frac{2}{10}$,则$1-\frac{1}{5}-\frac{1}{10}=\frac{10}{10}-\frac{2}{10}-\frac{1}{10}=\frac{10-2 - 1}{10}=\frac{7}{10}$。
【答案】:$1\frac{1}{10}$;$\frac{1}{6}$;$1$;$44\frac{4}{9}$;$\frac{2}{7}$;$\frac{3}{10}$;$\frac{7}{16}$;$\frac{7}{10}$
1. 计算$\frac{2}{5}+\frac{7}{10}$:
先通分,$\frac{2}{5}=\frac{2×2}{5×2}=\frac{4}{10}$,则$\frac{2}{5}+\frac{7}{10}=\frac{4}{10}+\frac{7}{10}=\frac{4 + 7}{10}=\frac{11}{10}=1\frac{1}{10}$。
2. 计算$\frac{5}{6}-\frac{2}{3}$:
先通分,$\frac{2}{3}=\frac{2×2}{3×2}=\frac{4}{6}$,则$\frac{5}{6}-\frac{2}{3}=\frac{5}{6}-\frac{4}{6}=\frac{5 - 4}{6}=\frac{1}{6}$。
3. 计算$\frac{11}{18}+\frac{7}{18}$:
同分母分数相加,分母不变,分子相加,$\frac{11}{18}+\frac{7}{18}=\frac{11 + 7}{18}=\frac{18}{18}=1$。
4. 计算$45-\frac{5}{9}$:
把$45$写成$44+\frac{9}{9}$,则$45-\frac{5}{9}=44+\frac{9}{9}-\frac{5}{9}=44+\frac{9 - 5}{9}=44\frac{4}{9}$。
5. 计算$\frac{1}{7}+\frac{2}{14}$:
先化简$\frac{2}{14}=\frac{1}{7}$,则$\frac{1}{7}+\frac{2}{14}=\frac{1}{7}+\frac{1}{7}=\frac{1+1}{7}=\frac{2}{7}$。
6. 计算$\frac{1}{2}-\frac{1}{5}$:
先通分,$\frac{1}{2}=\frac{1×5}{2×5}=\frac{5}{10}$,$\frac{1}{5}=\frac{1×2}{5×2}=\frac{2}{10}$,则$\frac{1}{2}-\frac{1}{5}=\frac{5}{10}-\frac{2}{10}=\frac{5 - 2}{10}=\frac{3}{10}$。
7. 计算$\frac{1}{4}+\frac{1}{8}+\frac{1}{16}$:
先通分,$\frac{1}{4}=\frac{1×4}{4×4}=\frac{4}{16}$,$\frac{1}{8}=\frac{1×2}{8×2}=\frac{2}{16}$,则$\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=\frac{4}{16}+\frac{2}{16}+\frac{1}{16}=\frac{4 + 2+1}{16}=\frac{7}{16}$。
8. 计算$1-\frac{1}{5}-\frac{1}{10}$:
先把$1$写成$\frac{10}{10}$,$\frac{1}{5}=\frac{1×2}{5×2}=\frac{2}{10}$,则$1-\frac{1}{5}-\frac{1}{10}=\frac{10}{10}-\frac{2}{10}-\frac{1}{10}=\frac{10-2 - 1}{10}=\frac{7}{10}$。
【答案】:$1\frac{1}{10}$;$\frac{1}{6}$;$1$;$44\frac{4}{9}$;$\frac{2}{7}$;$\frac{3}{10}$;$\frac{7}{16}$;$\frac{7}{10}$
(1)在( )里填上合适的质数。
$49= $(
$22= $(
$25= $(
$49= $(
7
)×(7
)$22= $(
2
)×(11
)$25= $(
5
)×(5
)
答案:
7,7;2,11;5,5
(2)8和9的最大公因数是(
1
),最小公倍数是(72
)。12和72的最大公因数是(12
),最小公倍数是(72
)。
答案:
1,72,12,72
(3)如图,用分数表示图中的阴影部分是(
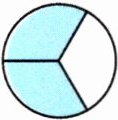
$\frac{2}{3}$
)。
答案:
$\frac{2}{3}$
(4)两个质数的最小公倍数是51,则这两个质数是(
3
)和(17
)。
答案:
$3$;$17$
(5)$\frac {9}{10}$米比(
$\frac{13}{10}$
)米短$\frac {2}{5}$米;比$\frac {4}{5}米长\frac {2}{20}$米的是($\frac{9}{10}$
)米。
答案:
$\frac{13}{10}$;$\frac{9}{10}$
3. 判断。(对的打“√”,错的打“×”)
(1)把两个一样的正方体拼成一个长方体后,体积和表面积都不变。 (
(2)一瓶矿泉有500升。 (
(3)有限小数都可以写成分母是10、100、1000…的分数。 (
(4)分数单位相同的分数才能直接相加减。 (
(5)$\frac {9}{10}$的分子减2,要使分数保持不变,应把分母也减2。 (
(1)把两个一样的正方体拼成一个长方体后,体积和表面积都不变。 (
×
)(2)一瓶矿泉有500升。 (
×
)(3)有限小数都可以写成分母是10、100、1000…的分数。 (
√
)(4)分数单位相同的分数才能直接相加减。 (
√
)(5)$\frac {9}{10}$的分子减2,要使分数保持不变,应把分母也减2。 (
×
)
答案:
(1)×
(2)×
(3)√
(4)√
(5)×
(1)×
(2)×
(3)√
(4)√
(5)×
4. 看右图填空。

(1)指针从“12”绕点A顺时针旋转$60^{\circ }$到“(
(2)指针从“12”绕点A顺时针旋转(
(3)指针从“1”绕点A顺时针旋转(

(1)指针从“12”绕点A顺时针旋转$60^{\circ }$到“(
2
)”;(2)指针从“12”绕点A顺时针旋转(
90°
)到“3”;(3)指针从“1”绕点A顺时针旋转(
150°
)到“6”。
答案:
(1)$2$;
(2)$90^{\circ}$;
(3)$150^{\circ}$。
(1)$2$;
(2)$90^{\circ}$;
(3)$150^{\circ}$。
5. 计算。
$1-\frac {2}{3}-\frac {1}{3}$
$\frac {1}{9}+\frac {4}{9}-\frac {4}{18}$
$1-\frac {2}{3}-\frac {1}{3}$
$\frac {1}{9}+\frac {4}{9}-\frac {4}{18}$
答案:
【解析】:
对于$1 - \frac{2}{3} - \frac{1}{3}$,根据减法的性质$a - b - c=a-(b + c)$,则$1-\frac{2}{3}-\frac{1}{3}=1-(\frac{2}{3}+\frac{1}{3})$,因为$\frac{2}{3}+\frac{1}{3}=\frac{2 + 1}{3}=1$,所以$1-(\frac{2}{3}+\frac{1}{3})=1 - 1=0$。
对于$\frac{1}{9}+\frac{4}{9}-\frac{4}{18}$,先计算同分母分数加法$\frac{1}{9}+\frac{4}{9}=\frac{1 + 4}{9}=\frac{5}{9}$,再将$\frac{5}{9}$和$\frac{4}{18}$通分,$\frac{5}{9}=\frac{5×2}{9×2}=\frac{10}{18}$,则$\frac{5}{9}-\frac{4}{18}=\frac{10}{18}-\frac{4}{18}=\frac{10 - 4}{18}=\frac{6}{18}=\frac{1}{3}$。
【答案】:$0$;$\frac{1}{3}$
对于$1 - \frac{2}{3} - \frac{1}{3}$,根据减法的性质$a - b - c=a-(b + c)$,则$1-\frac{2}{3}-\frac{1}{3}=1-(\frac{2}{3}+\frac{1}{3})$,因为$\frac{2}{3}+\frac{1}{3}=\frac{2 + 1}{3}=1$,所以$1-(\frac{2}{3}+\frac{1}{3})=1 - 1=0$。
对于$\frac{1}{9}+\frac{4}{9}-\frac{4}{18}$,先计算同分母分数加法$\frac{1}{9}+\frac{4}{9}=\frac{1 + 4}{9}=\frac{5}{9}$,再将$\frac{5}{9}$和$\frac{4}{18}$通分,$\frac{5}{9}=\frac{5×2}{9×2}=\frac{10}{18}$,则$\frac{5}{9}-\frac{4}{18}=\frac{10}{18}-\frac{4}{18}=\frac{10 - 4}{18}=\frac{6}{18}=\frac{1}{3}$。
【答案】:$0$;$\frac{1}{3}$
查看更多完整答案,请扫码查看


