2025年暑假作业与生活陕西师范大学出版总社有限公司七年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业与生活陕西师范大学出版总社有限公司七年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
数学智慧拼图
项目情境
为了缓解同学们的学习压力, 提高思维能力, 增强学习兴趣, 并促进同学们的全面发展。王老师将数学学习小组分成三组, 每组领取一些长方形卡片, 开展“数学智慧拼图”为主题的项目式学习。
任务一: 观察建模
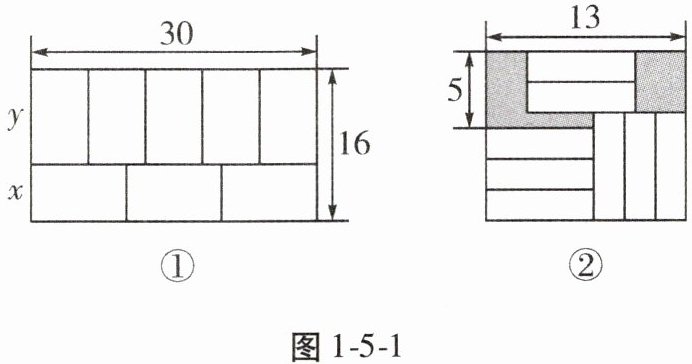
如图 1-5-1①, 第一小组领了 8 个大小、形状完全相同的小长方形, 拼成一个大长方形, 每个小长方形的长和宽分别为 $ y $, $ x $($ y > x $), 小组同学测得拼成的大长方形的长为 30, 宽为 16, 可得方程组 $ \begin{cases} 5x = 30, \\ x + y = 16, \end{cases} $ 则 $ x = $______, $ y = $______。
任务二: 推理分析
第二小组也领了 8 个大小、形状完全相同的小长方形, 把它们按图 1-5-1②所示的方式放置在一个大长方形中, 求图 1-5-1②中阴影部分的面积。
任务三: 设计方案
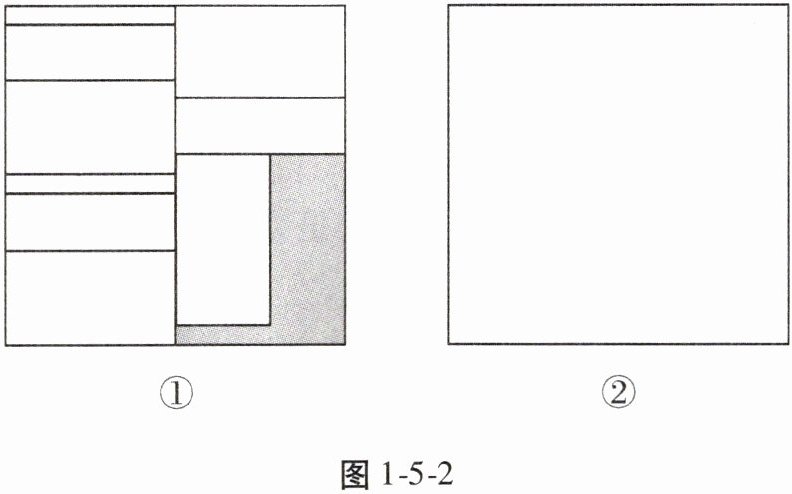
第三小组领了 A, B, C 三种类型的长方形卡片, 它们的长为 18, 宽分别为 $ a $, $ b $, $ c $, 其中 $ a < b < c $ 且 $ a $, $ b $, $ c $ 均为正整数, 分别取 A, B, C 卡片 2, 3, 4 张, 把它们按图 1-5-2①所示方式放置在一个边长为 36 的正方形中, 则阴影部分的面积为 144; 若分别取 A, B, C 卡片 3, 2, 5 张, 能否把它们放置在边长为 36 的正方形中(不能有重叠), 如果能, 请你在图 1-5-2②中画出放置好的示意图, 并标注 $ a $, $ b $, $ c $ 的值, 如果不能, 请说明原因。
项目情境
为了缓解同学们的学习压力, 提高思维能力, 增强学习兴趣, 并促进同学们的全面发展。王老师将数学学习小组分成三组, 每组领取一些长方形卡片, 开展“数学智慧拼图”为主题的项目式学习。
任务一: 观察建模
如图 1-5-1①, 第一小组领了 8 个大小、形状完全相同的小长方形, 拼成一个大长方形, 每个小长方形的长和宽分别为 $ y $, $ x $($ y > x $), 小组同学测得拼成的大长方形的长为 30, 宽为 16, 可得方程组 $ \begin{cases} 5x = 30, \\ x + y = 16, \end{cases} $ 则 $ x = $______, $ y = $______。

任务二: 推理分析
第二小组也领了 8 个大小、形状完全相同的小长方形, 把它们按图 1-5-1②所示的方式放置在一个大长方形中, 求图 1-5-1②中阴影部分的面积。
任务三: 设计方案
第三小组领了 A, B, C 三种类型的长方形卡片, 它们的长为 18, 宽分别为 $ a $, $ b $, $ c $, 其中 $ a < b < c $ 且 $ a $, $ b $, $ c $ 均为正整数, 分别取 A, B, C 卡片 2, 3, 4 张, 把它们按图 1-5-2①所示方式放置在一个边长为 36 的正方形中, 则阴影部分的面积为 144; 若分别取 A, B, C 卡片 3, 2, 5 张, 能否把它们放置在边长为 36 的正方形中(不能有重叠), 如果能, 请你在图 1-5-2②中画出放置好的示意图, 并标注 $ a $, $ b $, $ c $ 的值, 如果不能, 请说明原因。

答案:
解:任务一:已知$\begin{cases} 5x = 30, ① \\ x + y = 16, ② \end{cases}$
由①,得$x = 6$,
把$x = 6$代入②,得$y = 10$,
原方程组的解是$\begin{cases} x = 6, \\ y = 10。 \end{cases}$
故答案为6,10。
任务二:设8个大小、形状完全相同的小长方形长为$m$,宽为$n$,由题意,得
$\begin{cases} m + 3n = 13, \\ m + 2n - 3n = 5, \end{cases}$
解得$\begin{cases} m = 7, \\ n = 2, \end{cases}$
则阴影部分的面积为$13 \times (5 + 3 \times 2) - 8 \times 7 \times 2 = 31$。
任务三:由题意得,
$\begin{cases} 2 \times 18a + 3 \times 18b + 4 \times 18c + 144 = 36^2, \\ 2a + 2b + 2c = 36, \end{cases}$
解得$\begin{cases} b = 8 - 2a, \\ c = a + 10。 \end{cases}$
∵$a < b < c$且$a$,$b$,$c$均为正整数,
∴$\begin{cases} a < 8 - 2a, \\ 8 - 2a < a + 10, \end{cases}$
解得$0 < a < \frac{8}{3}$,
∴$a = 1$或2。
当$a = 2$时,$b = 8 - 2a = 4$,$c = a + 10 = 12$,
分别取A,B,C卡片3,2,5张,拼成的不重叠的图形面积为:
$3 \times 18 \times 2 + 2 \times 18 \times 4 + 5 \times 18 \times 12 = 1332 > 36^2$,
故此时不能放置;
当$a = 1$时,$b = 8 - 2a = 6$,$c = a + 10 = 11$,
分别取A,B,C卡片3,2,5张,拼成的不重叠的图形面积为:
$3 \times 18 \times 1 + 2 \times 18 \times 6 + 5 \times 18 \times 11 = 1260 < 36^2$,
故此时能放置,放置方式如下图:

解:任务一:已知$\begin{cases} 5x = 30, ① \\ x + y = 16, ② \end{cases}$
由①,得$x = 6$,
把$x = 6$代入②,得$y = 10$,
原方程组的解是$\begin{cases} x = 6, \\ y = 10。 \end{cases}$
故答案为6,10。
任务二:设8个大小、形状完全相同的小长方形长为$m$,宽为$n$,由题意,得
$\begin{cases} m + 3n = 13, \\ m + 2n - 3n = 5, \end{cases}$
解得$\begin{cases} m = 7, \\ n = 2, \end{cases}$
则阴影部分的面积为$13 \times (5 + 3 \times 2) - 8 \times 7 \times 2 = 31$。
任务三:由题意得,
$\begin{cases} 2 \times 18a + 3 \times 18b + 4 \times 18c + 144 = 36^2, \\ 2a + 2b + 2c = 36, \end{cases}$
解得$\begin{cases} b = 8 - 2a, \\ c = a + 10。 \end{cases}$
∵$a < b < c$且$a$,$b$,$c$均为正整数,
∴$\begin{cases} a < 8 - 2a, \\ 8 - 2a < a + 10, \end{cases}$
解得$0 < a < \frac{8}{3}$,
∴$a = 1$或2。
当$a = 2$时,$b = 8 - 2a = 4$,$c = a + 10 = 12$,
分别取A,B,C卡片3,2,5张,拼成的不重叠的图形面积为:
$3 \times 18 \times 2 + 2 \times 18 \times 4 + 5 \times 18 \times 12 = 1332 > 36^2$,
故此时不能放置;
当$a = 1$时,$b = 8 - 2a = 6$,$c = a + 10 = 11$,
分别取A,B,C卡片3,2,5张,拼成的不重叠的图形面积为:
$3 \times 18 \times 1 + 2 \times 18 \times 6 + 5 \times 18 \times 11 = 1260 < 36^2$,
故此时能放置,放置方式如下图:

查看更多完整答案,请扫码查看


