《2025年文轩图书假期生活指导暑八年级数学通用版》

11. 计算：$\sqrt{63} ÷ \sqrt{7} - | - 4 | = $$-1$.

答案： $-1$

12. 若式子$\frac{1}{\sqrt{x - 3}}$有意义,则实数$x$的取值范围是$x ＞ 3$.

答案： $x ＞ 3$

13. 计算$(\sqrt{19} + 1)(\sqrt{19} - 1)$的结果等于18.

答案： 18

14. 若$3 - \sqrt{2}$的整数部分为$a$,小数部分为$b$,则代数式$(2 + \sqrt{2}a) \cdot b$的值是______2.

答案： 2

15. 已知$m$为正整数,若$\sqrt{189m}$是整数,则根据$\sqrt{189m} = \sqrt{3 × 3 × 3 × 7m} = 3\sqrt{3 × 7m}$可知$m$有最小值$3 × 7 = 21$. 设$n$为正整数,若$\sqrt{\frac{300}{n}}$是大于1的整数,则$n$的最小值为3,最大值为75.

答案： 3 75

16. (1)计算：$| - 2\sqrt{2} | - 3^{-1} - \sqrt{4} × \sqrt{2} + (\pi - 5)^0$；
(2)计算：$\sqrt{27} ÷ \frac{\sqrt{3}}{2} × 2\sqrt{2} - 6\sqrt{2}$.

答案： 解：
(1) 原式 $= 2\sqrt{2} - \frac{1}{3} - 2\sqrt{2} + 1 = \frac{2}{3}$。
(2) 原式 $= 3\sqrt{3} × \frac{2}{\sqrt{3}} × 2\sqrt{2} - 6\sqrt{2}$
$= 12\sqrt{2} - 6\sqrt{2}$
$= 6\sqrt{2}$。

17. 解方程：$(\sqrt{3} + 1)(\sqrt{3} - 1)x = \sqrt{72} - \sqrt{18}$.

答案： $x = \frac{3\sqrt{2}}{2}$

18. 已知$a = 2 + \sqrt{5}$,$b = 2 - \sqrt{5}$,求代数式$a^2b + ab^2$的值.
-4

答案： 解：$\because a = 2 + \sqrt{5}$，$b = 2 - \sqrt{5}$，
$\therefore a^2b + ab^2$
$= ab(a + b)$
$= (2 + \sqrt{5})(2 - \sqrt{5})(2 + \sqrt{5} + 2 - \sqrt{5})$
$= (4 - 5) × 4$
$= -1 × 4$
$= -4$。

19. 如图,正方形$ABCD$的面积为8,正方形$ECFG$的面积为32.

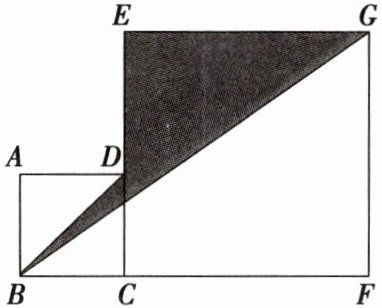
(1)求正方形$ABCD$和正方形$ECFG$的边长；
正方形$ABCD$的边长为$2\sqrt{2}$，正方形$ECFG$的边长为$4\sqrt{2}$；
(2)求阴影部分的面积.
阴影部分的面积为12.

答案： 解：
(1) 正方形 $ABCD$ 的边长为：$BC = \sqrt{8} = 2\sqrt{2}$，
正方形 $ECFG$ 的边长为：$CF = \sqrt{32} = 4\sqrt{2}$；
(2) $\because BC = 2\sqrt{2}$，$CF = 4\sqrt{2}$，
$\therefore BF = BC + CF = 6\sqrt{2}$；
$\therefore S_{\triangle BFG} = \frac{1}{2}GF \cdot BF = 24$；
又 $S_{\triangle ABD} = \frac{1}{2}AB \cdot AD = 4$，
$\therefore S_{阴影} = S_{正方形ABCD} + S_{正方形ECFG} - S_{\triangle BFG} -$
$S_{\triangle ABD} = 8 + 32 - 24 - 4 = 12$。

20. 数学课上,同学们对王老师黑板上的题很感兴趣,他们的答案都不同,且众说纷纭. 题目如下：
化简：$\sqrt{\frac{a}{bc}} + \sqrt{\frac{b}{ca}} + \sqrt{\frac{c}{ab}}$
①小浩说：当$a$,$b$,$c$皆为正数时,化简结果为$\frac{a + b + c}{abc}\sqrt{abc}$；
②小特说：当$a$,$b$,$c$皆为负数时,化简结果为$\frac{b - c - a}{abc}\sqrt{abc}$；
③小凌说：当$a ＜ 0$,$b ＞ 0$,$c ＜ 0$时,化简结果为$\frac{b - a - c}{abc}\sqrt{abc}$；
④小斯说：当$a ＞ 0$,$b ＜ 0$,$c ＜ 0$时,化简结果为$\frac{a - c - b}{abc}\sqrt{abc}$；
(1)以上同学的说法正确的是______①③④；
(2)请在这四个中任选两个判断其正确性.
选 ①② 判断如下：
① 当 $a$，$b$，$c$ 皆为正数时，
原式 $= \sqrt{\frac{a^2}{abc}} + \sqrt{\frac{b^2}{abc}} + \sqrt{\frac{c^2}{abc}}$
$= \frac{a}{\sqrt{abc}} + \frac{b}{\sqrt{abc}} + \frac{c}{\sqrt{abc}}$
$= \frac{a + b + c}{abc}\sqrt{abc}$
故 ① 正确。
② 当 $a$，$b$，$c$ 皆为负数时，$\frac{a}{bc} ＜ 0$，$\sqrt{\frac{a}{bc}}$ 无意义，
$\therefore$ ② 错误。

答案： 解：
(1) ① 当 $a$，$b$，$c$ 皆为正数时，
原式 $= \sqrt{\frac{a^2}{abc}} + \sqrt{\frac{b^2}{abc}} + \sqrt{\frac{c^2}{abc}}$
$= \frac{a}{\sqrt{abc}} + \frac{b}{\sqrt{abc}} + \frac{c}{\sqrt{abc}}$
$= \frac{a + b + c}{abc}\sqrt{abc}$。
故 ① 正确。
② 当 $a$，$b$，$c$ 皆为负数时，$\frac{a}{bc} ＜ 0$，$\sqrt{\frac{a}{bc}}$ 无意义，
$\therefore$ ② 错误。
③ 当 $a ＜ 0$，$b ＞ 0$，$c ＜ 0$ 时，
原式 $= \sqrt{\frac{a^2}{abc}} + \sqrt{\frac{b^2}{abc}} + \sqrt{\frac{c^2}{abc}}$
$= \frac{-a}{\sqrt{abc}} + \frac{b}{\sqrt{abc}} + \frac{-c}{\sqrt{abc}}$
$= \frac{b - a - c}{\sqrt{abc}}$
$= \frac{b - a - c}{abc}\sqrt{abc}$。
$\therefore$ ③ 正确。
④ 当 $a ＞ 0$，$b ＜ 0$，$c ＜ 0$ 时，
原式 $= \sqrt{\frac{a^2}{abc}} + \sqrt{\frac{b^2}{abc}} + \sqrt{\frac{c^2}{abc}}$
$= \frac{a}{\sqrt{abc}} + \frac{-b}{\sqrt{abc}} + \frac{-c}{\sqrt{abc}}$
$= \frac{a - b - c}{\sqrt{abc}}$
$= \frac{a - b - c}{abc}\sqrt{abc}$
$\therefore$ ①③④ 正确。
故答案为：①③④。
(2) 选 ①② 判断如下：
① 当 $a$，$b$，$c$ 皆为正数时，
原式 $= \sqrt{\frac{a^2}{abc}} + \sqrt{\frac{b^2}{abc}} + \sqrt{\frac{c^2}{abc}}$
$= \frac{a}{\sqrt{abc}} + \frac{b}{\sqrt{abc}} + \frac{c}{\sqrt{abc}}$
$= \frac{a + b + c}{abc}\sqrt{abc}$
故 ① 正确。
② 当 $a$，$b$，$c$ 皆为负数时，$\frac{a}{bc} ＜ 0$，$\sqrt{\frac{a}{bc}}$ 无意义，
$\therefore$ ② 错误。