《2025年文轩图书假期生活指导暑八年级数学通用版》

1. 如图, 在平行四边形 $ABCD$ 中, 将 $\triangle ABC$ 沿着 $AC$ 所在的直线翻折得到 $\triangle AB'C$, $B'C$ 交 $AD$ 于点 $E$, 连接 $B'D$. 若 $\angle B = 60^{\circ}$, $\angle ACB = 45^{\circ}$, $AC = \sqrt{6}$, 则 $B'D$ 的长是(B)

A.1
B.$\sqrt{2}$
C.$\sqrt{3}$
D.$\frac{\sqrt{6}}{2}$

答案： B

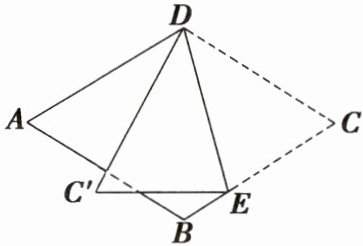
2. 如图, 在菱形纸片 $ABCD$ 中, $\angle A = 60^{\circ}$, 点 $E$ 在 $BC$ 边上, 将菱形纸片 $ABCD$ 沿 $DE$ 折叠, 点 $C$ 的对应点为点 $C'$, 且 $DC'$ 垂直平分 $AB$, 则 $\angle DEC$ 为(D)

A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$75^{\circ}$

答案： D

3. 如图, 四边形 $ABCD$ 为正方形, 点 $E$ 是 $BC$ 的中点, 将正方形 $ABCD$ 沿 $AE$ 折叠, 得到点 $B$ 的对应点为点 $F$, 延长 $EF$ 交线段 $DC$ 于点 $P$, 若 $AB = 6$, 则 $DP$ 的长度为____2.

答案： 2

4. 如图, 一张矩形纸片 $ABCD$, 将点 $B$ 折叠到对角线 $AC$ 上的点 $M$ 处, 折痕 $CE$ 交 $AB$ 于点 $E$. 将点 $D$ 折叠到对角线 $AC$ 上的点 $H$ 处, 折痕 $AF$ 交 $DC$ 于点 $F$.

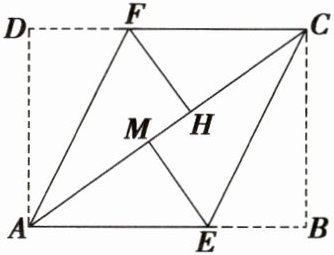
(1) 求证: $AF // CE$;
证明:∵四边形ABCD为矩形，
∴AD//BC,∴∠DAC=∠BCA.
由折叠知∠DAF=∠HAF=$\frac{1}{2}$∠DAC,∠BCE =∠MCE=$\frac{1}{2}$∠BCA,
∴∠HAF=∠MCE,∴AF//CE.
(2) 当∠BAC的大小为30°时, 四边形AECF是菱形? 请说明理由.
理由如下:
∵四边形ABCD是矩形，
∴∠B=∠BAD=90°,AB//CD,
由(1)知AF//CE,
∴四边形AECF是平行四边形.
要使四边形AECF是菱形,
则AE=EC,即∠EAC=∠ECA.
由折叠可得∠ECA=∠ECB,
∴∠BAC=∠ECA=∠ECB,
∴∠BAC=30°.

答案： 解:
(1)证明:
∵四边形ABCD为矩形，
∴AD//BC,
∴∠DAC=∠BCA.
由折叠知∠DAF=∠HAF=$\frac{1}{2}$∠DAC,∠BCE =∠MCE=$\frac{1}{2}$∠BCA,
∴∠HAF=∠MCE,
∴AF//CE.
(2)当∠BAC=30°时，四边形AECF是菱形.
理由如下:
∵四边形ABCD是矩形，
∴∠B=∠BAD=90°,AB//CD,
由
(1)知AF//CE,
∴四边形AECF是平行四边形.
要使四边形AECF是菱形,
则AE=EC,即∠EAC=∠ECA.
由折叠可得∠ECA=∠ECB,
∴∠BAC=∠ECA=∠ECB,
∴∠BAC=30°.